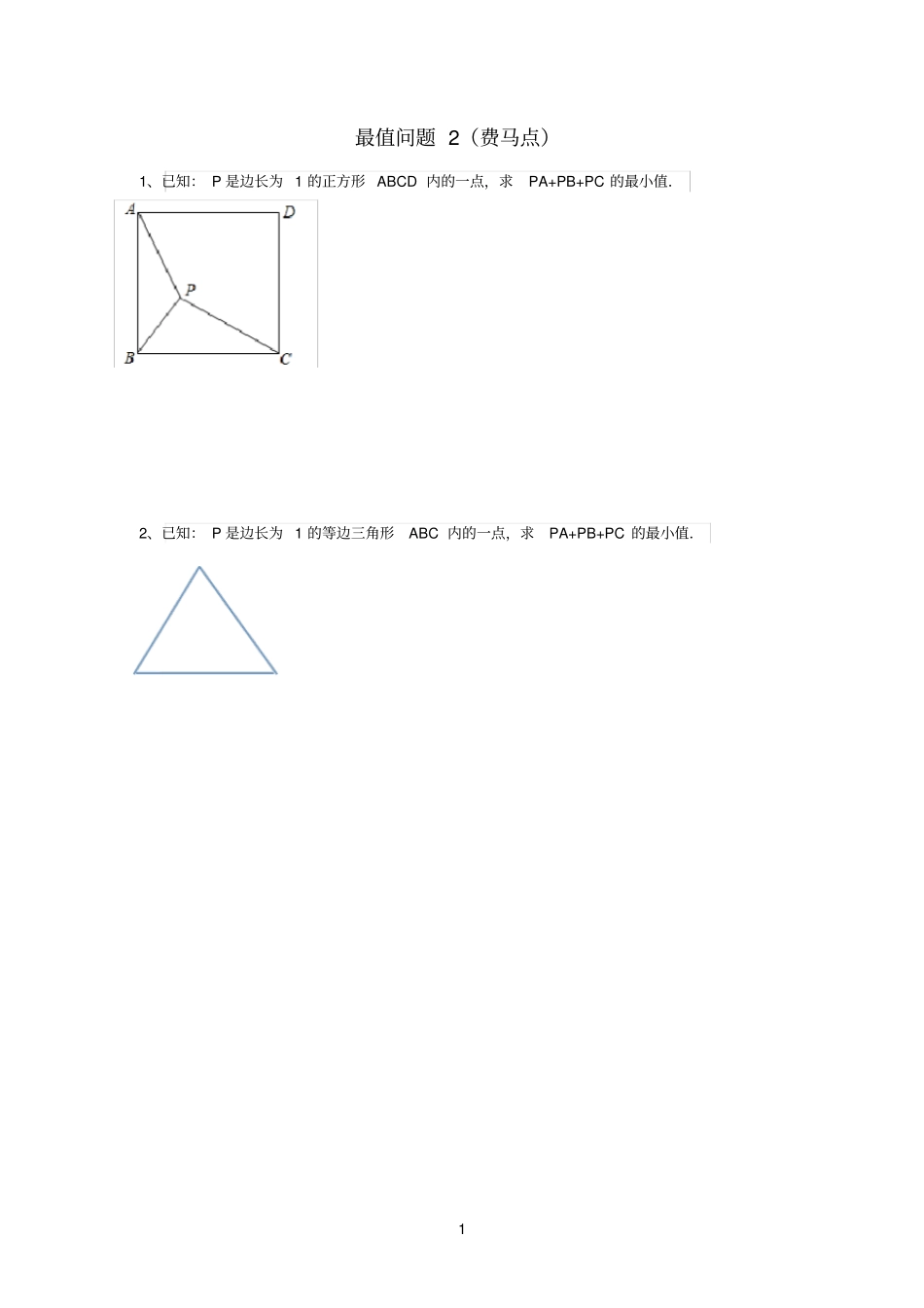
1最值问题 2(费马点)1、已知: P 是边长为 1 的正方形 ABCD 内的一点,求PA+PB+PC 的最小值.2、已知: P 是边长为 1 的等边三角形ABC 内的一点,求PA+PB+PC 的最小值.2图 2图 1A'PPAABCBC3、(延庆)(本题满分4 分)阅读下面材料:阅读下面材料:小伟遇到这样一个问题:如图1,在△ ABC (其中∠ BAC是一个可以变化的角)中, AB=2 ,AC=4 ,以 BC 为边在 BC 的下方作等边△PBC,求 AP 的最大值。小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B 为旋转中心将△ABP 逆时针旋转60°得到△ A’BC,连接AA',当点 A 落在CA'上时 ,此题可解(如图2).请你回答: AP 的最大值是.参考小伟同学思考问题的方法,解决下列问题:如图 3,等腰 Rt△ABC .边 AB=4,P 为△ ABC 内部一点,则 AP+BP+CP 的最小值是.(结果可以不化简)图3CABP34、(朝阳二模 )阅读下列材料:小华遇到这样一个问题,如图1,△ABC 中,∠ ACB=30o,BC=6,AC=5,在△ABC 内部有一点P,连接 PA、PB、PC,求 PA+PB+PC 的最小值 .小华是这样思考的:要解决这个问题, 首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点 C 顺时针旋转60o,得到 △EDC,连接 PD、BE,则 BE 的长即为所求 .(1)请你写出图2 中, PA+PB+PC 的最小值为;(2)参考小华的思考问题的方法,解决下列问题:①如图 3,菱形 ABCD 中,∠ ABC=60o,在菱形ABCD 内部有一点P,请在图3中画出并指明长度等于PA+PB+PC 最小值的线段(保留画图痕迹, 画出一条即可) ;②若①中菱形ABCD 的边长为 4,请直接写出当PA+PB+PC 值最小时 PB 的长.DEACBP图 2 DACB图 3 ACBP图 1 45、(海淀二模)如图 . 在平面直角坐标系xOy 中. 点 B 的坐标为 (0,2). 点 D 在 x 轴的正半轴上 . 30ODB. OE 为△ BOD 的中线 . 过 B 、 E 两点的抛物线236yaxxc 与x 轴相交于 A 、F 两点 (A 在 F 的左侧 ). (1) 求抛物线的解析式;(2) 等边 △ OMN 的顶点 M 、 N 在线段 AE 上. 求 AE 及 AM 的长;(3) 点 P 为△ ABO内的一个动点 . 设 mPAPBPO . 请直接写出 m 的最小值 , 以及 m 取得最小值时 , 线段 AP 的长 . (备用图 )