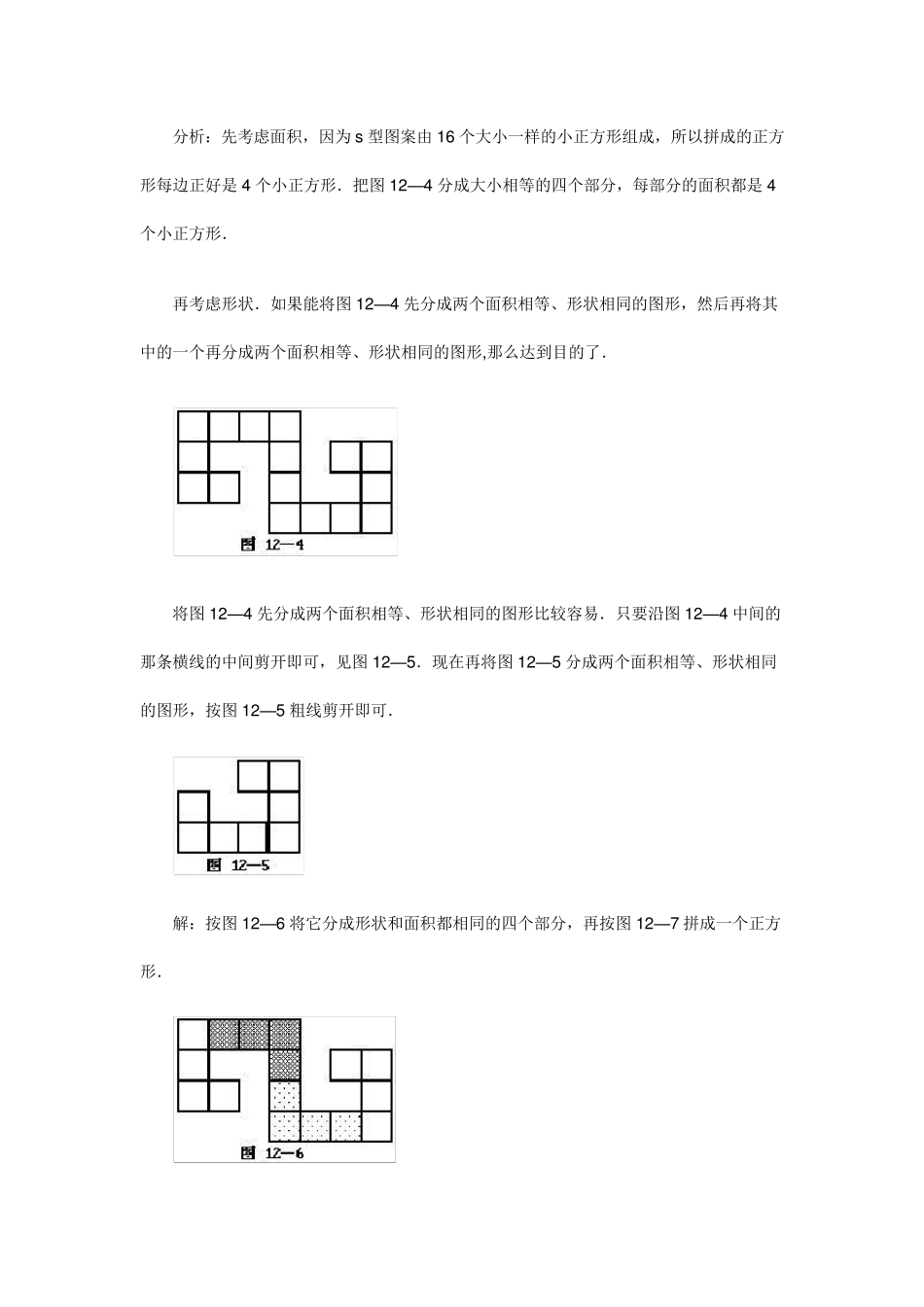
图形的分割与组合 图形的分割与组合是几何学中一个非常有趣味的课题,研究图形的分割与组合问题不仅可以增强几何图形的直观感觉和判断能力,丰富对图形的想象力,提高数学的思维能力,而且还有一定的实用价值,对工厂里的下料、工艺美术的图案设计都有一定的用处. 例 1 将图1 2 —1 所示的图形分成两块,然后拼成一个正方形. 图1 2 —1 分析:如果我们假设每个小正方形的边长是1 个单位,要拼成的正方形的面积为 1 6 ,所以边长为 4 .而这个缺角的长方形的长为 6 ,宽为 3 ,切分后将右边向左平移 2 个单位,再向上平移 1 个单位,作切分时应注意到缺角的特点. 解:沿图1 2 —2 中的粗线将原图分割开,把右块推至左块之上,拼成一个边长为 4 的正方形,如图1 2 —3 . 例 2 将图1 2 —4 中的图形分成四个形状相同,大小相等的四个部分,然后拼成一个正方形. 分析:先考虑面积,因为s 型图案由16 个大小一样的小正方形组成,所以拼成的正方形每边正好是4 个小正方形.把图12—4 分成大小相等的四个部分,每部分的面积都是4个小正方形. 再考虑形状.如果能将图12—4 先分成两个面积相等、形状相同的图形,然后再将其中的一个再分成两个面积相等、形状相同的图形,那么达到目的了. 将图12—4 先分成两个面积相等、形状相同的图形比较容易.只要沿图12—4 中间的那条横线的中间剪开即可,见图12—5.现在再将图12—5 分成两个面积相等、形状相同的图形,按图12—5 粗线剪开即可. 解:按图12—6 将它分成形状和面积都相同的四个部分,再按图12—7 拼成一个正方形. 例3 有一块长6 米、宽 3 米的长方形地毯,现要把它放到长4 .5 米、宽 4 米的房间中,能否将它剪成形状相同,大小相等的两块,使其正好铺满房间. 分析:因为原地毯的长比要拼成的长方形的长多 1 .5 米,宽少 1 米,所以我们将原地毯分成长1 .5 米、宽 1 米的小长方形,如图 1 2 —8 .这样分成 1 2 个小长方形.因为新的长方形的长为 4 .5 米、宽 4 米,长应减少一个小长方形,宽应增 加一个小长方形.可以沿对角线的方向把它剪成呈阶梯状的两块,并使它们的形状和大小完全相同,如图 1 2 —9 ,然后把它们错位对齐,这样拼成了一个新的长方形,如图 1 2 —1 0 . 解:按图 1 2 —9 中的粗线将长方形分成两块,然后错位对齐,即可拼成新的长方形,见图 1 2 —1 0 . ...