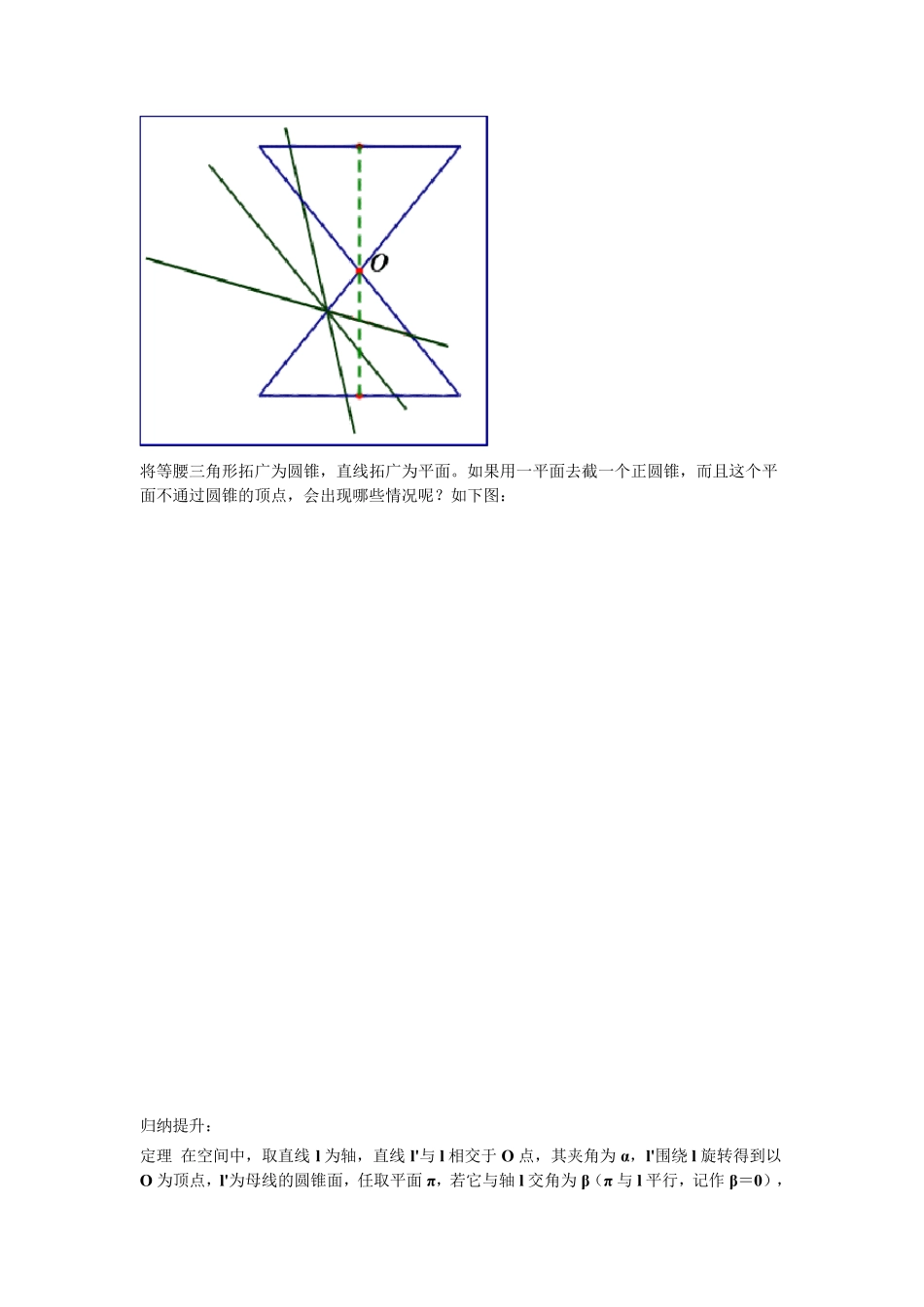
平 面 与圆锥面 的截线 一、直观感受: 观察平面截圆锥面的图形,截线是什么图形? 改变平面的位置,可得到三种曲线,它们统称为圆锥曲线(下图由软件《立几画板》制作): 二、分类探究: 从平面图形入手,开始讨论一条直线与等腰三角形的位置关系: 将等腰三角形拓广为圆锥,直线拓广为平面。如果用一平面去截一个正圆锥,而且这个平面不通过圆锥的顶点,会出现哪些情况呢?如下图: 归纳提升: 定理 在空间中,取直线l为轴,直线l'与 l相交于 O 点,其夹角为α,l'围绕 l旋转得到以O 为顶点,l'为母线的圆锥面,任取平面π,若它与轴 l交角为β(π 与 l平行,记作 β=0),则: (1)β>α,平面π 与圆锥的交线为椭圆; (2)β=α,平面π 与圆锥的交线为抛物线; (3)β<α,平面π 与圆锥的交线为双曲线。 三、证明结论: 利用 Dan delin 双球(这两个球位于圆锥的内部,一个位于平面的上方,一个位于平面的下方,并且与平面及圆锥均相切)证明:β>α,平面与圆锥的交线为椭圆. 如图,利用切线长相等,容易证明 PF1+PF2=PQ1+PQ2=Q1Q2=定值. 下面证明:β=α 时,平面与圆锥面的交线为抛物线。 下面讨论当平面与圆锥面的交线为双曲线时准线的及离心率: 换个角度看图: 容易知道:截得的圆锥曲线的离心率等于截面和圆锥轴的夹角的余弦与圆锥顶角一半的余弦之比. 四、知识运用 用图霸制作三维直观图: 解答参看下图: 五、图形制作 三种曲线的丹迪林 Dandelin 双球图可以在《几何图霸》中统一到一幅图中,主要制作步骤如下: 1.作全自由点 O,过点 O 作平行于 z 轴上的点 B,过 B 作平行于 x 轴上的点 C,作点 B、C关于 O 的对称点 B’、C'. 2.选取点 O、B、C,作圆锥,选取点 O、B’、C’,作圆锥. 3.在圆B 上任取点D,作D 关于B 对称点,连接O D,OD’,在O D 上任取一点E,以E为圆心画过点D’、D 的心点圆,在圆E 上任取点F,连EF,它表示截面的位置,可以绕点E 转动. 4.作角 O EF 的平分线,与轴 BB’交于O 1;作角 DEF 的平分线,与轴 BB’交于O 2,它们就是双球的球心. 5.过球心O 1、O 2 分别作边 EF 的垂线,垂足分别为 F1、F2,它们就是焦点. 6.选取点 O 1、F1,作球O 1(图中显示大圆,光照后显示为球),同法作球O 2. 7.取线 EF 上的点 G、H,作 GDO 垂线上的伸缩点 I,作点 I 关于点 G 的对称点 I’,按...