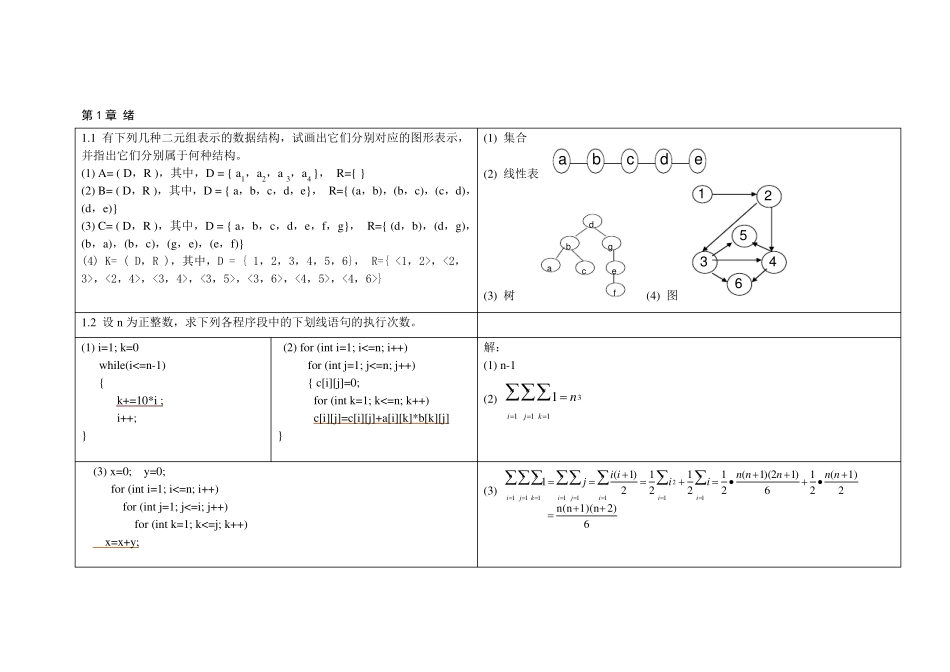
第1 章 绪 1.1 有下列几种二元组表示的数据结构,试画出它们分别对应的图形表示,并指出它们分别属于何种结构。 (1) A= ( D,R ),其中,D = { a1,a2,a 3,a4 }, R={ } (2) B= ( D,R ),其中,D = { a,b,c,d,e}, R={ (a,b),(b,c),(c,d),(d,e)} (3) C= ( D,R ),其中,D = { a,b,c,d,e,f,g}, R={ (d,b),(d,g),(b,a),(b,c),(g,e),(e,f)} (4) K= ( D,R ),其中,D = { 1,2,3,4,5,6}, R={ <1,2>,<2,3>,<2,4>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>} (1) 集合 (2) 线性表 abcde (3) 树 fgabcde (4) 图 145362 1.2 设 n 为正整数,求下列各程序段中的下划线语句的执行次数。 (1) i=1; k=0 while(i<=n-1) { k+=10*i ; i++; } (2) for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) { c[i][j]=0; for (int k=1; k<=n; k++) c[i][j]=c[i][j]+a[i][k]*b[k][j] } 解: (1) n-1 (2) ninjnkn11131 (3) x=0; y=0; for (int i=1; i<=n; i++) for (int j=1; j<=i; j++) for (int k=1; k<=j; k++) x=x+y; (3) 62)1)(nn(n 21)(216)12)(1(21 21212)1(1112111111•• nnnnniiiijnininiijjkniijni 1.3 指出下列个算法的功能,并求其时间复杂度。 (1) int sum1(int n) { int p=1,s=0; for (int i=1;i<=n; i++) { p*= i; s+=p;} return s; } (2) int sum2 (int n) { int s=0; for ( int i=1; i<=n; i++) { int p=1; for (int j=1; j<=i; j++) p*=j; s+=p; } return s; } 解: (1) n1ii! , T(n)=O(n) (2) n1ii! , T(n)=O(n2) 1.4 算法设计 有3 枚硬币,其中有1 枚是假的,伪币与真币重量略有不同。如何借用一架天平,找出伪币?以流程图表示算法。 上机练习题 要求:给出问题分析、算法描述、源程序及运行截图,在线提交。 1. 设 a, b, c 为 3 个整数,求其中位于中间值的整数。 开始A=B?A=C?A是伪币C是伪币B是伪币结束是是否否第2 章 线性表 1. 设计算法:在顺序表中删除值为e 的元素,删除成功,返回1;否则,返回0。 int Sqlist::DeleteElem( T e ) { for (i=1; i<=length; i++) // 按值顺序查找 *...