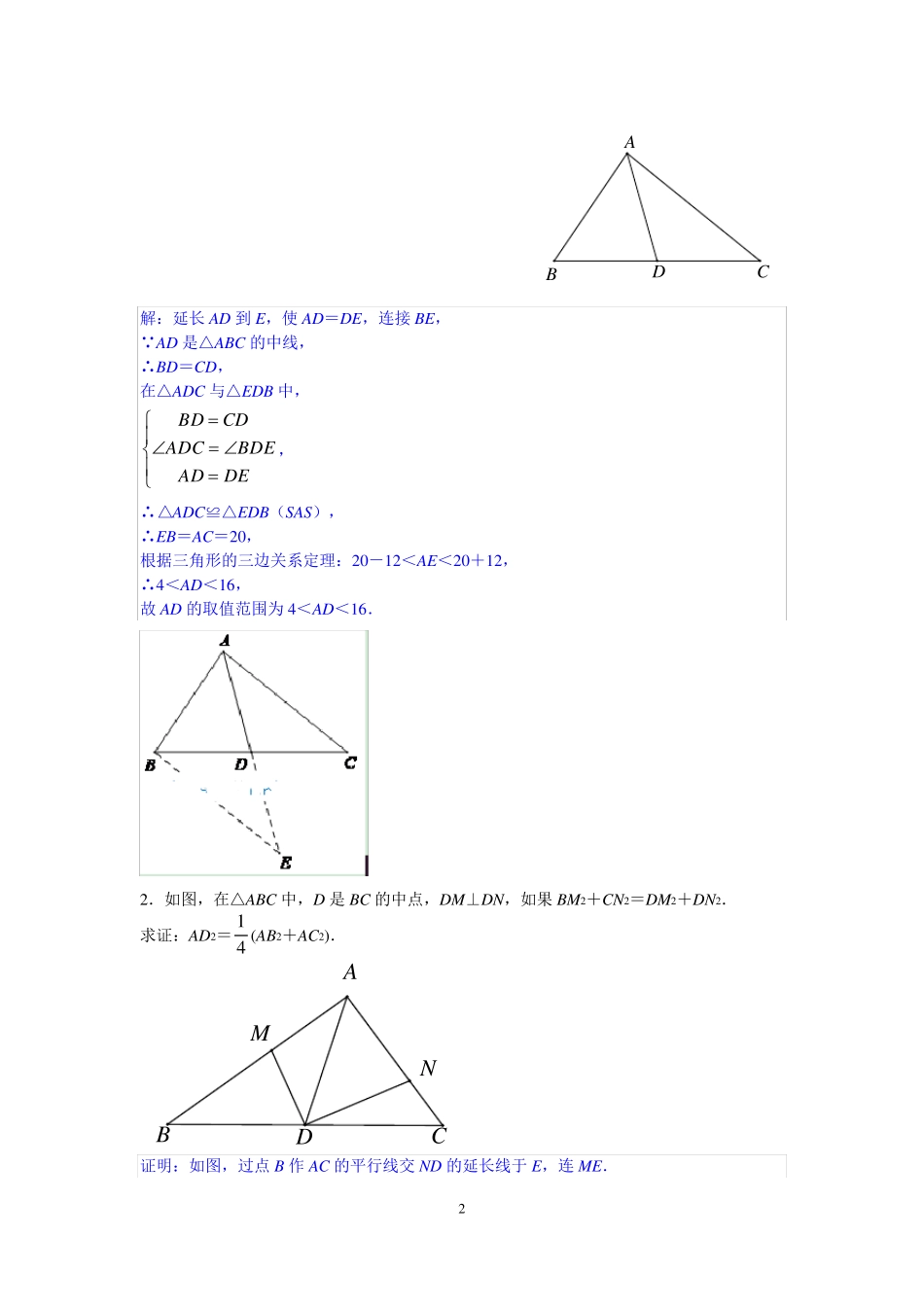
1 中点四大模型 模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 ②图①图构造全等倍长类中线倍长中线EEDCBAFFABCDABCDDCBA 模型分析 如图①,AD 是△ABC 的中线,延长AD 至点E 使DE=AD,易证:△ADC≌△EDB(SAS). 如图②,D 是BC 中点,延长FD 至点E 使DE=FD,易证:△FDB≌△EDC(SAS) 当遇见中线或者中点的时候,可以尝试倍长中线或类中线,构造全等三角形,目的是对已知条件中的线段进行转移. 模型实例 如图,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,连接 BE 并延长交AC 于点F,AF=EF,求证:AC=BE. FEDCBA 1 .如图,在△ABC 中,AB=1 2 ,AC=2 0 ,求 BC 边上中线AD 的范围. 2 DCBA 解:延长AD 到E,使AD=DE,连接BE, AD 是△ABC 的中线, ∴BD=CD, 在△ADC 与△EDB 中, DEADBDEADCCDBD, ∴△ADC≌△EDB(SAS), ∴EB=AC=2 0 , 根据三角形的三边关系定理:2 0 -1 2 <AE<2 0 +1 2 , ∴4 <AD<1 6 , 故 AD 的取值范围为 4 <AD<1 6 . 2 .如图,在△ABC 中,D 是BC 的中点,DM⊥DN,如果 BM2+CN2=DM2+DN2. 求证:AD2=41(AB2+AC2). NMDCBA 证明:如图,过点 B 作 AC 的平行线交 ND 的延长线于 E,连ME. 3 BD=DC, ∴ED=DN. 在△BED 与△CND 中, DNEDCDNBDEDCBD ∴△BED≌△CND(SAS). ∴BE=NC. ∠MDN=90°, ∴MD 为EN 的中垂线. ∴EM=MN. ∴BM2+BE2=BM2+NC2=MD2+DN2=MN2=EM2, ∴△BEM 为直角三角形,∠MBE=90°. ∴∠ABC+∠ACB=∠ABC+∠EBC=90°. ∴∠BAC=90°. ∴AD2=( 21BC)2=41(AB2+AC2). 模型2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. 连接中线ABCDDCBA 模型分析 等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形“三线合一”的性质得4 到角相等,为解题创造更多的条件,当看见等腰三角形的时候,就应想到: “边等、角等、三线合一”. 模型实例 如图,在△ABC 中,AB=AC=5,BC=6,M 为BC 的中点,MN⊥AC 于点N,求MN的长度. NMCBA ABCMN 解答: 连接AM. AB=AC=5,BC=6,点M 为BC 中点, ∴AM⊥BC,BM=CM=21BC=3. AB=5, ∴AM=4352222 BMAB. MN⊥AC, ∴S△ANC=21MC·A...