中职数学指数函数与对数函数VIP免费

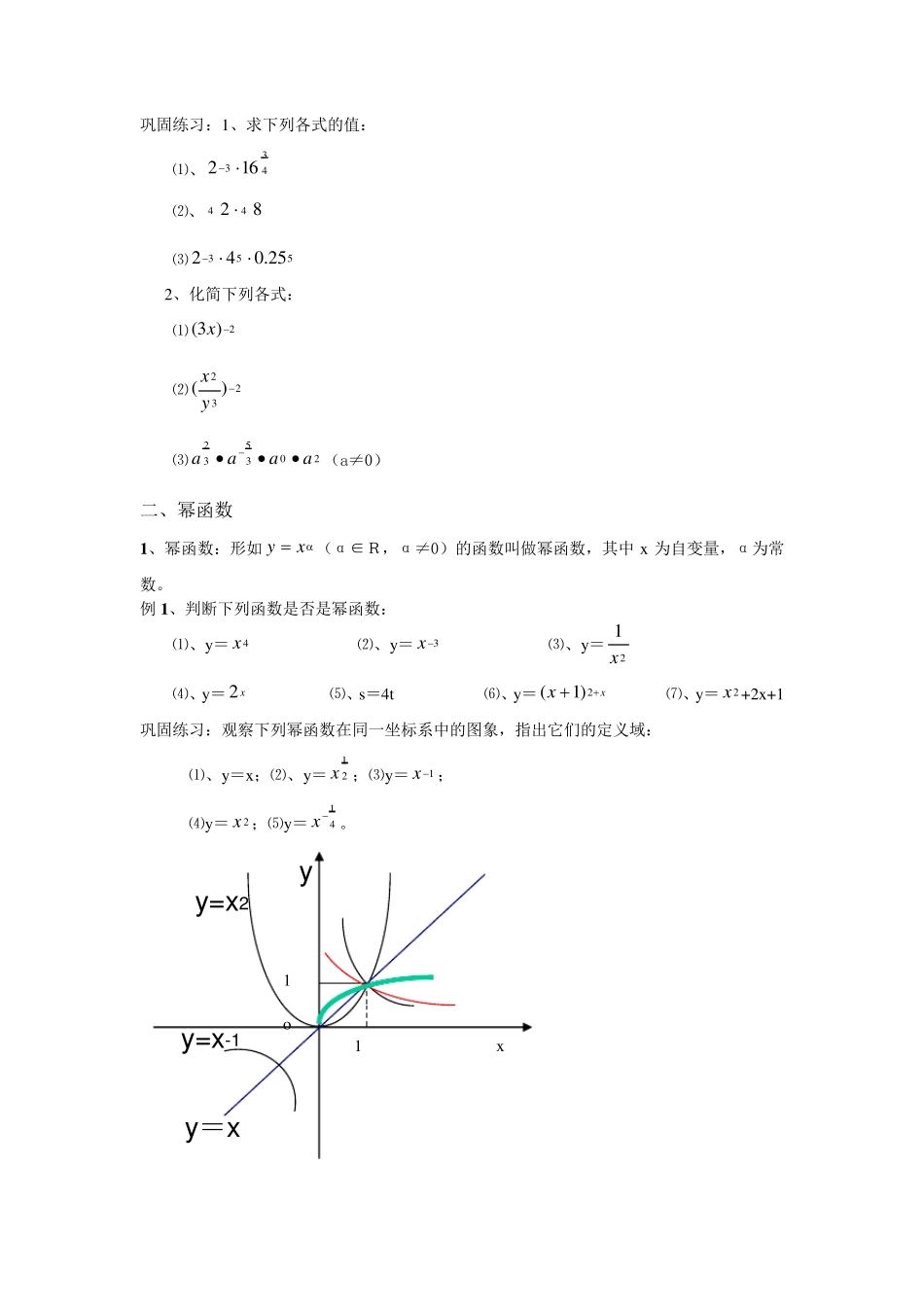
指数函数与对数函数 一、实数指数幂 1 、实数指数幂：如果xn=a（n∈N 且n＞1），则称x 为a 的n 次方根。当n 为奇数时，正数a 的n 次方根是一个正数，负数的n 次方根是一个负数。这时，a 的n 次方根只有一个，记作n a 。当n 为偶数时，正数a 的n 次方根有两个，它们互为相反数，分别记作n a ，－n a 。它们可以写成± n a 的形式。负数没有 （填“奇”或“偶”）次方根。 例：填空： （1）、（3 8 ）3= ；（38）3= 。 （2）338= ； 33)8(= 。 （3）、445 = ； 44)5(= 。 巩固练习： 1、将下列各分数指数幂写成根式的形式： （1）32a （2）53b（b≠0） 2、将下列各根式写成分数指数幂的形式： （1）52a （2）351a（a≠0） 3、求下列幂的值： （1）、（-5）0； （2）、（a-b）0； (3)、2-1； （4）、（4 7 ）4。 2 、实数指数幂的运算法则 ①、 aa •＝a ②、aa＝a ③、 )(a＝a ④、)(ab＝ba• ⑤、)(ba＝ba 例 1 ：求下列各式的值： ⑴、21100 ⑵、328 ⑶323188 • 例 2 ：化简下列各式： ⑴、3 aa ⑵、633333•• 巩固练习：1、求下列各式的值： ⑴、433 162 ⑵、4482  ⑶55325.042 2、化简下列各式： ⑴2)3(x ⑵232 )(yx ⑶203532aaaa•••（a≠0） 二、幂函数 1 、幂函数：形如xy （α∈Ｒ，α≠0）的函数叫做幂函数，其中 x 为自变量，α为常数。 例 1 、判断下列函数是否是幂函数： ⑴、y ＝4x ⑵、y ＝3x ⑶、y ＝21x ⑷、y ＝x2 ⑸、s＝4t ⑹、y ＝xx2)1( ⑺、y ＝2x +2x +1 巩固练习：观察下列幂函数在同一坐标系中的图象，指出它们的定义域： ⑴、y ＝x ；⑵、y ＝21x ；⑶y ＝1x； ⑷y ＝2x ；⑸y ＝41x。 o x 1 1 y y＝x y=x-1 y=x2 三、指数函数 1 、指数函数：形如y＝xa （a＞0,且a≠1）的函数叫做指数函数，其中x 为自变量，a 为常数，指数函数的定义域为R。 例1：判断下列函数是不是指数函数？ (1)xy)3( (2)43xy  （3）21xy  （4）xy52 (5) y＝x2 (6) y＝x)21( 2、指数函数性质归纳 函数 y＝xa （a＞1） y＝xa （0＜a＜1） 图 象 性 质 定义域 R 值域 (0，＋∞) 过定点 （０,１） 单调性 是R 上的增函数 是R 上的减函数 例1：已知指...