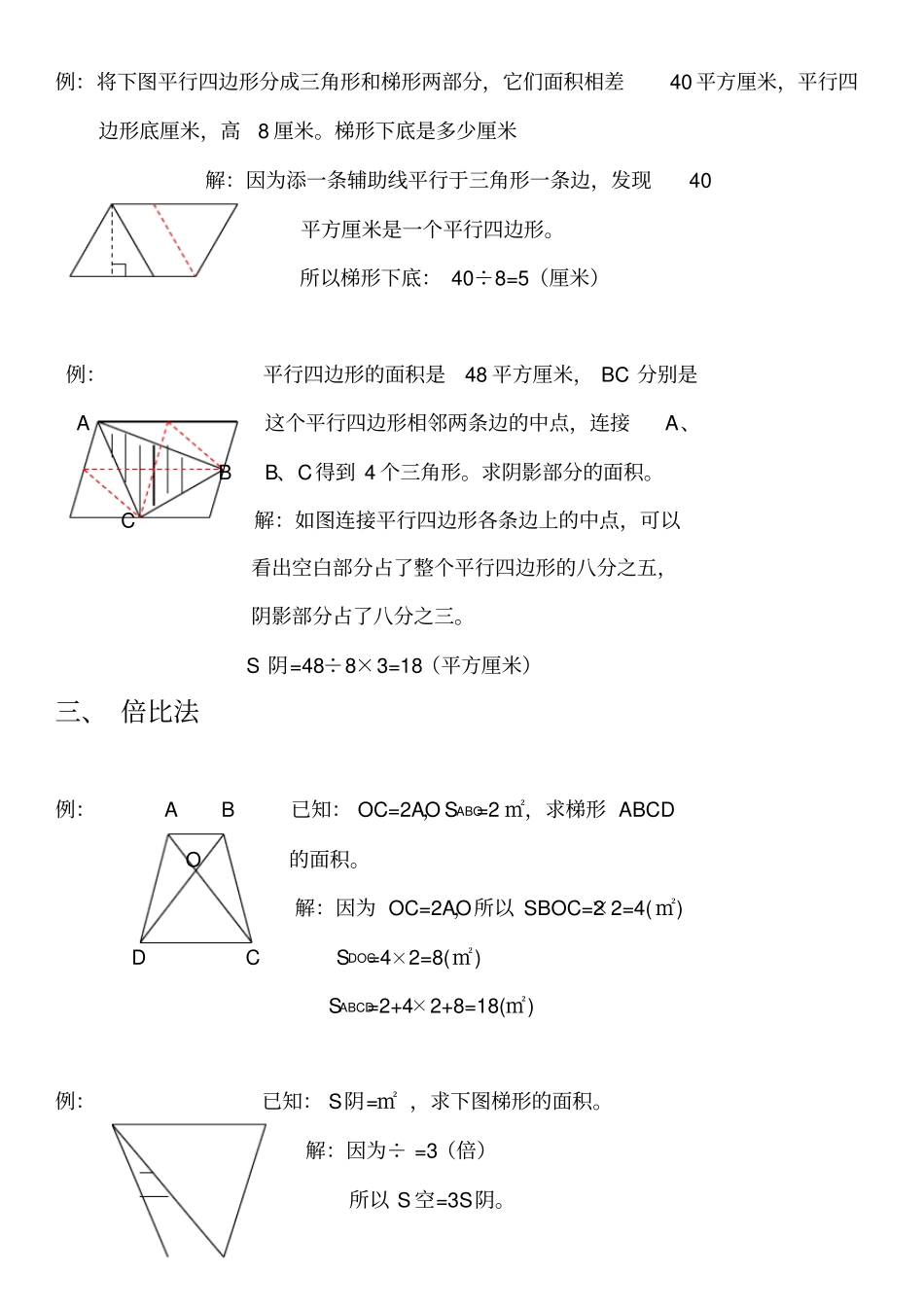
几何图形的十大解法(30 例)体会:注重积累,勤动笔。在平时的教学中,无论看到的、听到的、想到的、捕捉到的,灵感的一刹那都及时记下,并附上自己的一些想法和体会。虚心好学,勤动口。无论是老教师还是青年教师,本校教师还是外校、外地老师,能者都是我的老师,学生也是我的老师。我的一些巧解有的就来自于学生。在与老师、学生的互动中提高自己的解题能力。善于总结, 勤动脑。 在备课时, 经常分析学生解题中的一些想法和方法,找到学生最容易接受、理解的方法。同时我尽可能掌握本题的不同解法,以获得答案较为简洁的方法和策略。说明:1)首先要以扎实的几何基础知识为铺垫,才能提升灵活解题的技能技巧。2)以下十种解法是不全面的,更谈不上是最好的。唯有在实践中不断摸索、总结,找到适合自己的解题方法,才能不断创新。 追求是永无止境的。一、 分割法例:将两个相等的长方形重合在一起,求组合图形的面积。(单位:厘米) 2 解:将图形分割成两个全等的梯形。7S组=(7-2+7)×2÷2×2=24(平方厘米)例:下列两个正方形边长分别为8 厘米和 5 厘米,求阴影部分面积。解:将图形分割成3 个三角形。S=5×5÷2+5×8÷2+(8-5 )×5÷2 =+20+=38(平方厘米)例:左图中两个正方形的边长分别为8 厘米和 6 厘米。求阴影部分面积。解:将阴影部分分割成两个三角形。 S阴=8×(8+6)÷2+8×6÷2 =56+24 =80(平方厘米)二、 添辅助线例:已知正方形边长4 厘米, A、B、C、D 是正方形边上的中点, P 是任意一点。求阴影部分面积。C 解:从 P 点向 4 个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。P S 阴=4×4÷2=8(平方厘米)D B A 例:将下图平行四边形分成三角形和梯形两部分,它们面积相差40 平方厘米,平行四边形底厘米,高8 厘米。梯形下底是多少厘米解:因为添一条辅助线平行于三角形一条边,发现40 平方厘米是一个平行四边形。所以梯形下底: 40÷8=5(厘米)例:平行四边形的面积是48 平方厘米, BC 分别是A 这个平行四边形相邻两条边的中点,连接A、B B、C得到 4 个三角形。求阴影部分的面积。C 解:如图连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。 S 阴=48÷8×3=18(平方厘米)三、 倍比法例:A B 已知: OC=2AO,SABO=2 ㎡,求梯形 ABCDO 的面积。解:因为 OC=2AO,所以 SBOC=2×2=4( ㎡)...