平面和平面平行的性质-课件VIP免费

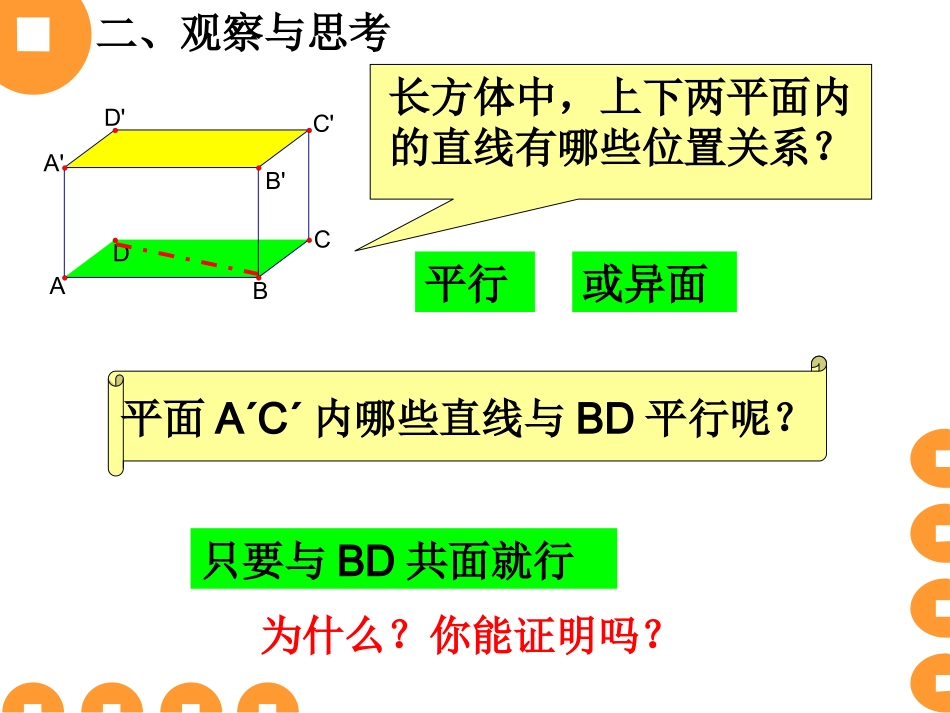
DA1B1D1C1BCA一、复习回顾1.两平面位置关系相交平行有一条公共直线没有公共点2.两平面平行的判定若一平面内两相交直线都与另一平面平行，则这两平面平行线//面面//面反之：要证面//面，只需找平行于另一平面的两相交直线思路二、观察与思考D'CB'ABA'DC'平行或异面平面A´C´内哪些直线与BD平行呢？长方体中，上下两平面内的直线有哪些位置关系？只要与BD共面就行为什么？你能证明吗？D'CB'ABA'DC'D'CB'ABA'DC'EFEF如图：长方体中，平面A´C´内的直线EF与BD共面，求证：EF//DB证明：EF平面A´C´BD//A´C´EF与BD无交点EF与BD共面EF//BD两平面平行的性质定理两平面平行的性质定理如果两个平行平面同时与第三个平面相交，那么它们的交线平行。思考：两平面平行的性质定理与线面平行的性质定理有什么不同？定理形成即：baba////简记:面面平行，则线线平行三、练习巩固1.判断下列命题的真假1)//,//,////mnmn3)//,//ll2)//,,//abab（假）（真）（真）2.设，表示两个不重合的平面，则下面条件中能推出//的一个是A)内有无数条直线与平行B)、与一条直线所成的角相等C)内有两条不平行且不重合的直线都与平行D)，与同一条直线距离相等例1：求证夹在两平行平面间的两条平行线段相等。已知：aβ∥AB和DC为夹在a、β间的平行线段。求证：AB＝DCADCB证明：可作平面，过CD//ABDCABADBC////BCAD//ABCDABCD为平行四边形ABCD例2.三棱锥A-BCD中，M，N分别是⊿ABC和⊿ACD的重心，求证：MN//平面BCD。ABCDMNFEG分析：由重心定理：23AmANAGAE在AC上取点F使AF:AC=3:2连NF、MF则FN//CE,FM//CG故面MNF//面BCD用了哪个结论？四、练习提高1.经过平面外两点，作与平行的平面，则这样的平面可以作A）1个或2个B)0个或1个C)1个D)0个2.若面//面，直线a//,点B，则在内过点B的所有直线中有___与a平行的直线A)存在唯一一条B)只有两条C)不一定存在D)存在无数条3.判断下列命题是否正确1）如果直线a//b,那么a平行于过b的任何平面2）若直线a//平面，那么a平行内的任何直线3）若直线a//平面，直线b//平面，那么a//b4）若直线a//b,a//平面,b,那么b//例4如图，平面、、γ两两平行，且直线与、、γ分别相交于点A、B、C，直线m与、、γ分别相交于点D、E、F，AB＝6，BC＝2，EF＝3，求DE的长。mABCEDFmABCEDFG五、小结直线//直线直线//平面平面//平面面面平行的性质面面平行的性质你能自己接着完成吗？六、作业1.如果一个直线与两个平行平面中的一个平行，那么这条直线与另一平面的位置关系是A)平行B)相交C)在平面内D)平行或在平面内2.如图所示，已知平面//平面，点P是平面,外的一点，且直线PB,PD分别与,相交于A,B与C,D（1）求证AC//BD（2）如果PA=4,AB=5,PC=3，求PD的长CAPBD3.四棱锥P-ABCD的底面是梯形，且AB//CD，DC=2AB，M是PC边的中点，求证：BM//平面PADPABCDMN用两种方法求解4.四棱锥P-ABCD底面是平行四边形，E,F分别是AB和PC的中点，求证：EF//平面PADPABCDEF9111578,FMCABMNADCDBFFEAMMNNBSEND5.如图，平面，线段分别交、于、，线段分别交、于、。线段分别交、于、，若，，，求的面积。AFCDB