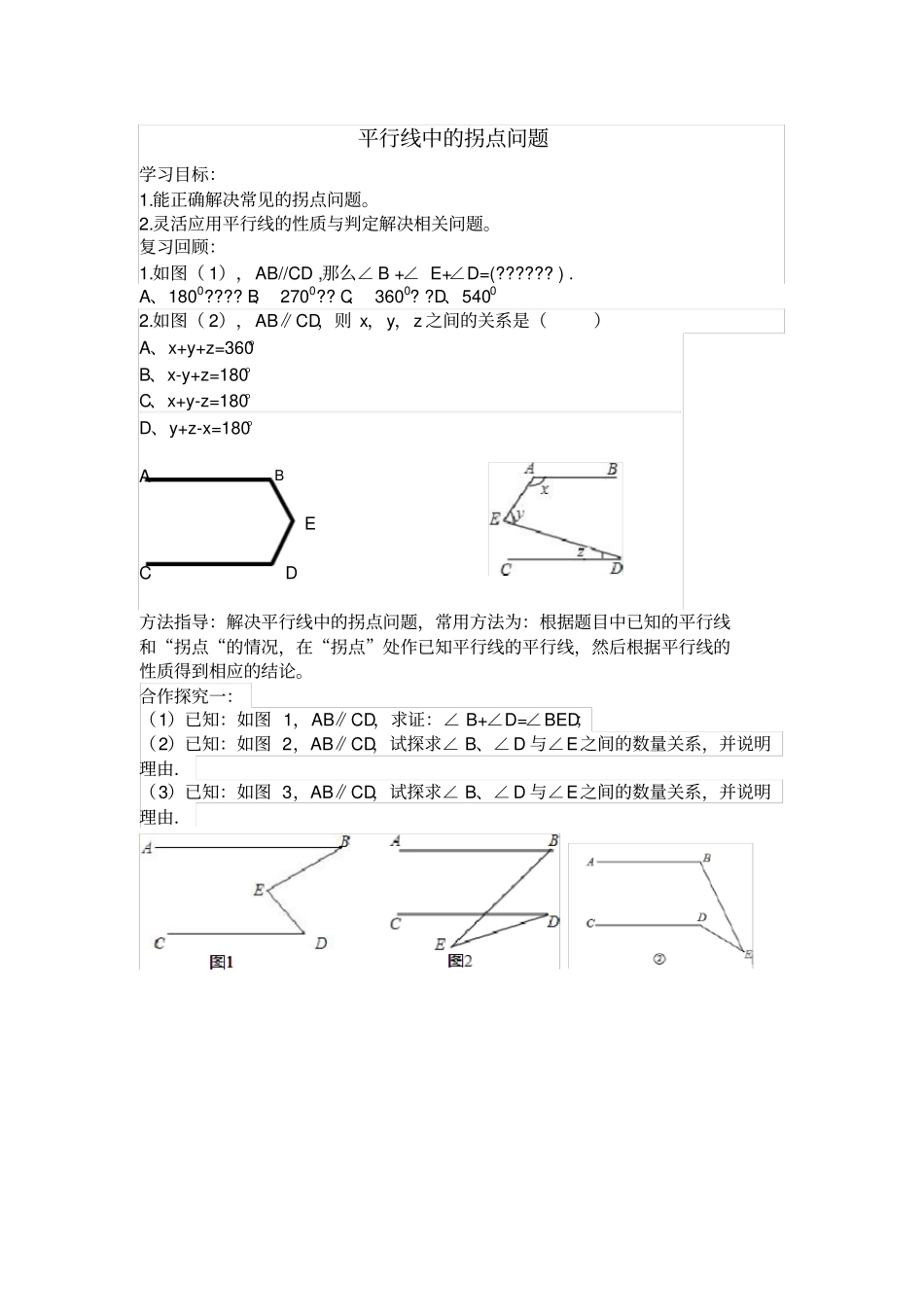
平行线中的拐点问题学习目标:1.能正确解决常见的拐点问题。2.灵活应用平行线的性质与判定解决相关问题。复习回顾:1.如图( 1),AB//CD ,那么∠ B +∠ E+∠D=(?????? ) .A、1800???? B、 2700?? C、 3600? ?D、54002.如图( 2),AB∥CD,则 x,y,z 之间的关系是()A、x+y+z=360°B、x-y+z=180°C、x+y-z=180°D、y+z-x=180°AEC D方法指导:解决平行线中的拐点问题,常用方法为:根据题目中已知的平行线和“拐点“的情况,在“拐点”处作已知平行线的平行线,然后根据平行线的性质得到相应的结论。合作探究一:(1)已知:如图 1,AB∥CD,求证:∠ B+∠D=∠BED;(2)已知:如图 2,AB∥CD,试探求∠ B、∠ D 与∠E之间的数量关系,并说明理由.(3)已知:如图 3,AB∥CD,试探求∠ B、∠ D 与∠E之间的数量关系,并说明理由.B 合作探究二:已知:如图, AB//CD,试解决下列问题:(1)∠ 1+∠2=______;? (2)∠ 1+∠2+∠3=_____;(3)∠ 1+∠2+∠3+∠4=_____;(4)试探究∠ 1+∠2+∠3+∠4+⋯+∠n=(??? )。跟踪练习:如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角 ∠A 是 105 度,第二次拐的角 ∠B 是 135 度,第三次拐的角是 ∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=.课堂小结:如何解决平行线中的拐点问题?当堂检测:1.如图,直线 l1∥l 2,∠A=125°,∠B=85°,则 ∠1+∠2=()A.30° B.35° C.36° D.40°2.如图,已知 AC∥BD,∠CAE=30°,∠DBE=35°,则∠AEB等于()A.30° B.45° C.65° D.75°拓展提升: 如图,已知 AB∥DE,BF,EF分别平分 ∠ABC与∠CED,若∠BCE=140° ,求∠BFE的度数.