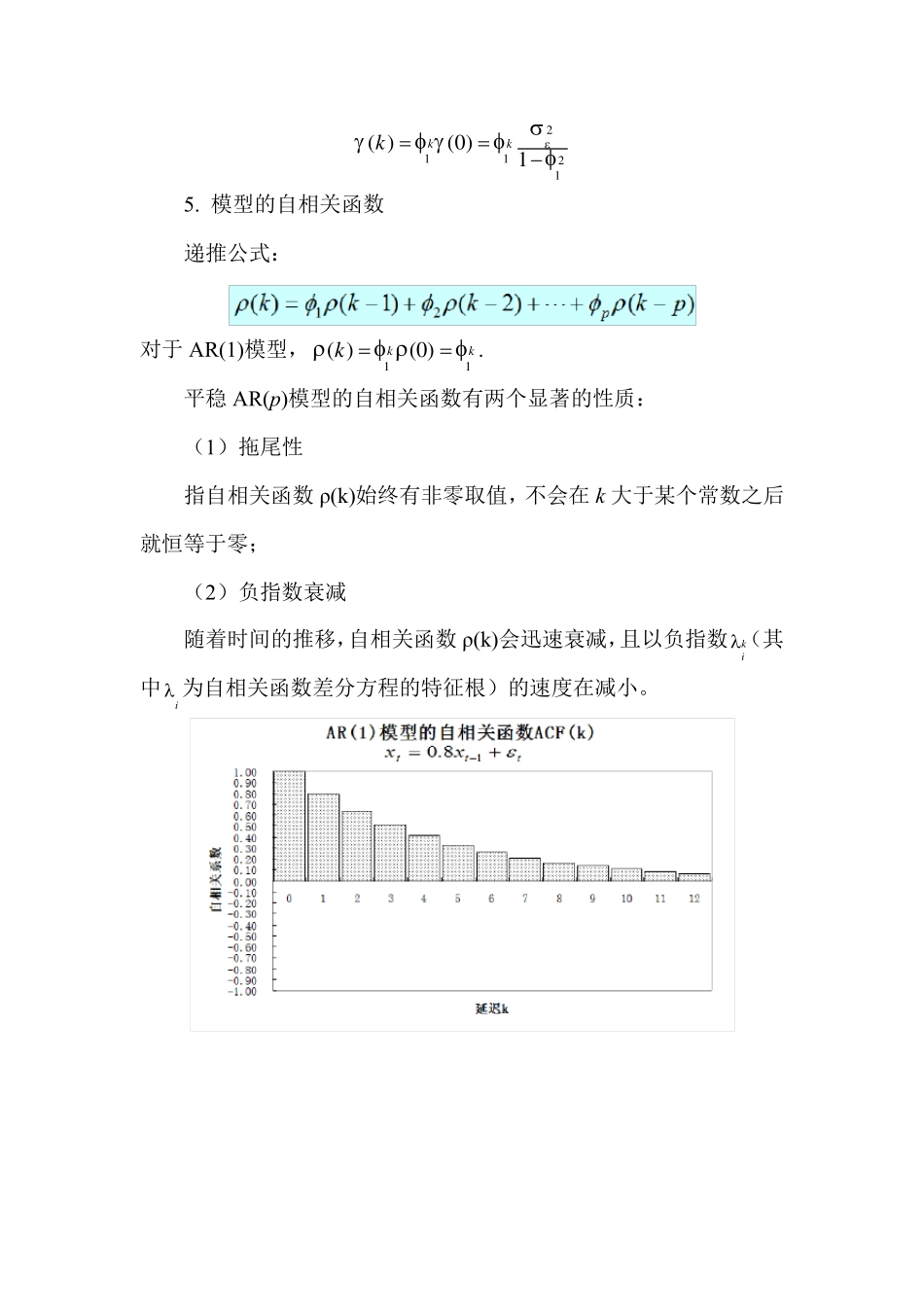
39. 时间序列分析Ⅱ——ARIMA 模型 随着对时间序列分析方法的深入研究,人们发现非平稳序列的确定性因素分解方法(如季节模型、趋势模型、移动平均、指数平滑等)只能提取显著的确定性信息,对随机性信息浪费严重,同时也无法对确定性因素之间的关系进行分析。 而非平稳序列随机分析的发展就是为了弥补确定性因素分解方法的不足。时间序列数据分析的第一步都是要通过有效手段提取序列中所蕴藏的确定性信息。Box 和 Jenkins 使用大量的案例分析证明差分方法是一种非常简便有效的确定性信息的提取方法。而 Gramer 分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。 (一)ARMA 模型 即自回归移动平均移动模型,是最常用的拟合平稳时间序列的模型,分为三类:AR 模型、MA 模型和 ARMA 模型。 一、AR(p)模型——p阶自回归模型 1. 模型: 011ttpt ptxxx 其中,0p ,随机干扰序列εt 为 0 均值、2 方差的白噪声序列(()0tsE , t≠s),且当期的干扰与过去的序列值无关,即 E(xtεt)=0. 由于是平稳序列,可推得均值011p. 若00 ,称为中心化的AR(p)模型,对于非中心化的平稳时间序列,可以令01(1)p,*ttxx转化为中心化。 记 B 为延迟算子,1( )pppBIBB称为p 阶自回归多项式,则 AR(p)模型可表示为:( )pttB x. 2. 格林函数 用来描述系统记忆扰动程度的函数,反映了影响效应衰减的快慢程度(回到平衡位置的速度),Gj 表示扰动 ε t-j 对系统现在行为影响的权数。 例如,AR(1)模型(一阶非齐次差分方程),1 , 0 ,1 ,2 ,jjGj 模型解为0tjtjjxG . 3. 模型的方差 对于AR(1)模型,22201()()1tjtjjVar xG Var. 4. 模型的自协方差 对中心化的平稳模型,可推得自协方差函数的递推公式: 用格林函数显示表示: 2000( )()ijtjt kjj kjijjkG G EGG 对于AR(1)模型, 21121( )(0 )1kkk 5. 模型的自相关函数 递推公式: 对于AR(1)模型,11( )(0 )kkk . 平稳AR(p)模型的自相关函数有两个显著的性质: (1)拖尾性 指自相关函数ρ(k)始终有非零取值,不会在k 大于某个常数之后就恒等于零; (2)负指数衰减 随着时间的推移,自...