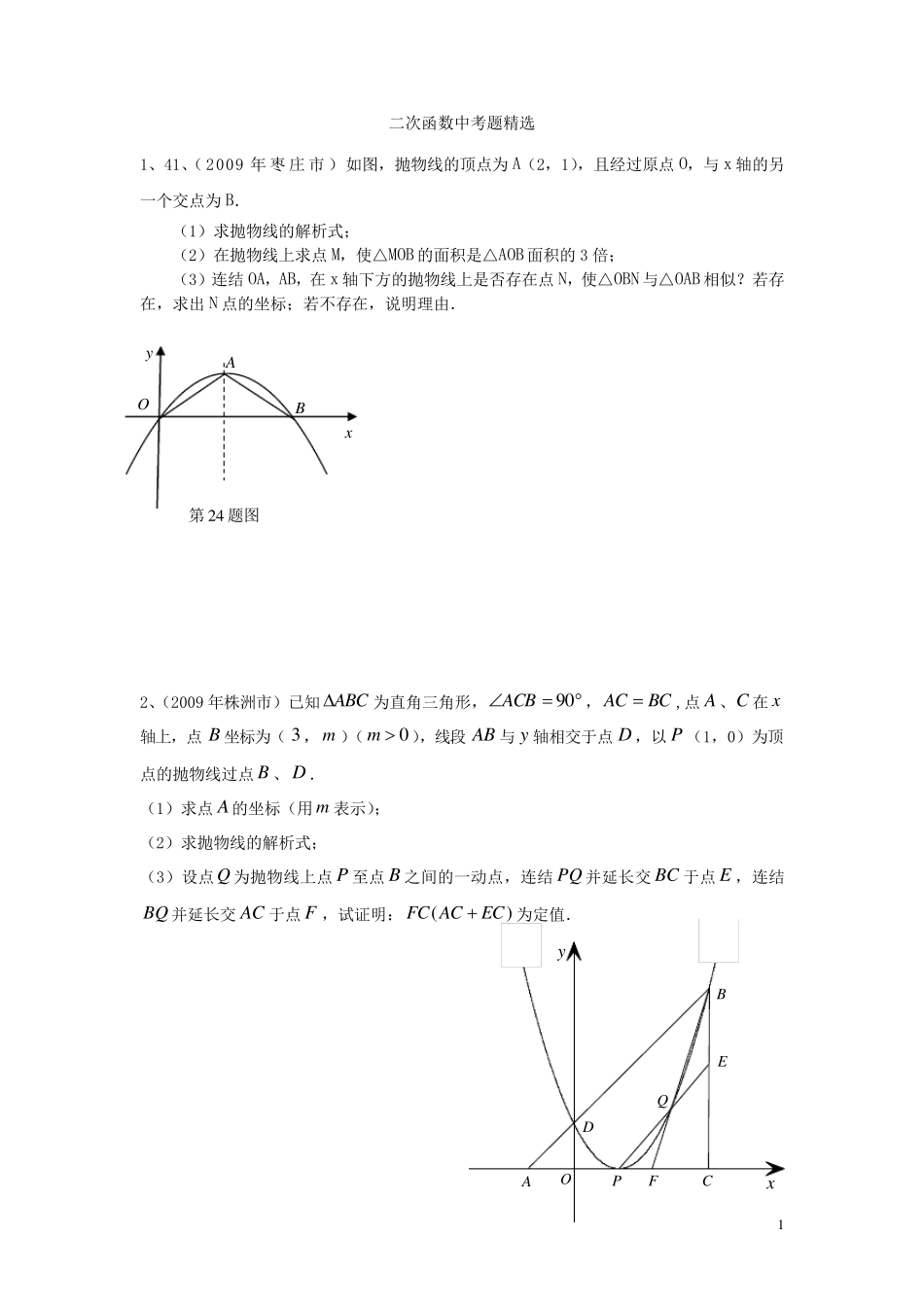
1 二次函数中考题精选 1、41、(2009 年枣庄市)如图,抛物线的顶点为A(2,1),且经过原点O,与x 轴的另一个交点为B. (1)求抛物线的解析式; (2)在抛物线上求点M,使△MOB 的面积是△AOB 面积的3 倍; (3)连结 OA,AB,在x 轴下方的抛物线上是否存在点N,使△OBN 与△OAB 相似?若存在,求出 N 点的坐标;若不存在,说明理由. 2、(2009 年株洲市)已知 ABC为直角三角形,90ACB ,ACBC,点A 、C 在x轴上,点B 坐标为(3 ,m )(0m ),线段 AB 与y轴相交于点D ,以 P (1,0)为顶点的抛物线过点B 、D . (1)求点A 的坐标(用m 表示); (2)求抛物线的解析式; (3)设点Q 为抛物线上点P 至点B 之间的一动点,连结 PQ 并延长交BC 于点E ,连结 BQ 并延长交AC 于点F ,试证明:()FC ACEC为定值. yxQPFEDCBAO y x O A B 第 2 4 题图 2 3、(2009 年重庆市江津区)某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20 元,并且每周(7 天)涨价2 元,从第6 周开始,保持每件30 元的稳定价格销售,直到11 周结束,该童装不再销售。 (1)请建立销售价格y(元)与周次x 之间的函数关系; (2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x 之间的关系为1 2)8(812 xz, 1≤ x ≤11,且x 为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少? 4、(2009 年重庆市江津区)抛物线cbxxy2与x 轴交与A(1,0),B(- 3,0)两点, (1)求该抛物线的解析式; (2)设(1)中的抛物线交 y 轴与C 点,在该抛物线的对称轴上是否存在点 Q,使得△QAC的周长最小?若存在,求出 Q 点的坐标;若不存在,请说明理由. (3)在(1)中的抛物线上的第二象限上是否存在一点 P,使△PBC 的面积最大?,若存在,求出点 P 的坐标及△PBC 的面积最大值.若没有,请说明理由. 3 5、(2009 年滨州) 如图①,某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成,在等腰梯形ABCD 中,ABDC∥,20cm30cm45ABDCADC,,°.对于抛物线部分,其顶点为CD 的中点O ,且过 AB、两点,开口终端的连线MN 平行且等于 DC . (1)如图①所示,在以点O 为原点,直线OC 为 x 轴的坐标系内,点C 的坐标为(15 0),, 试求 AB...