中考数学二次函数压轴题讲义有答案VIP免费

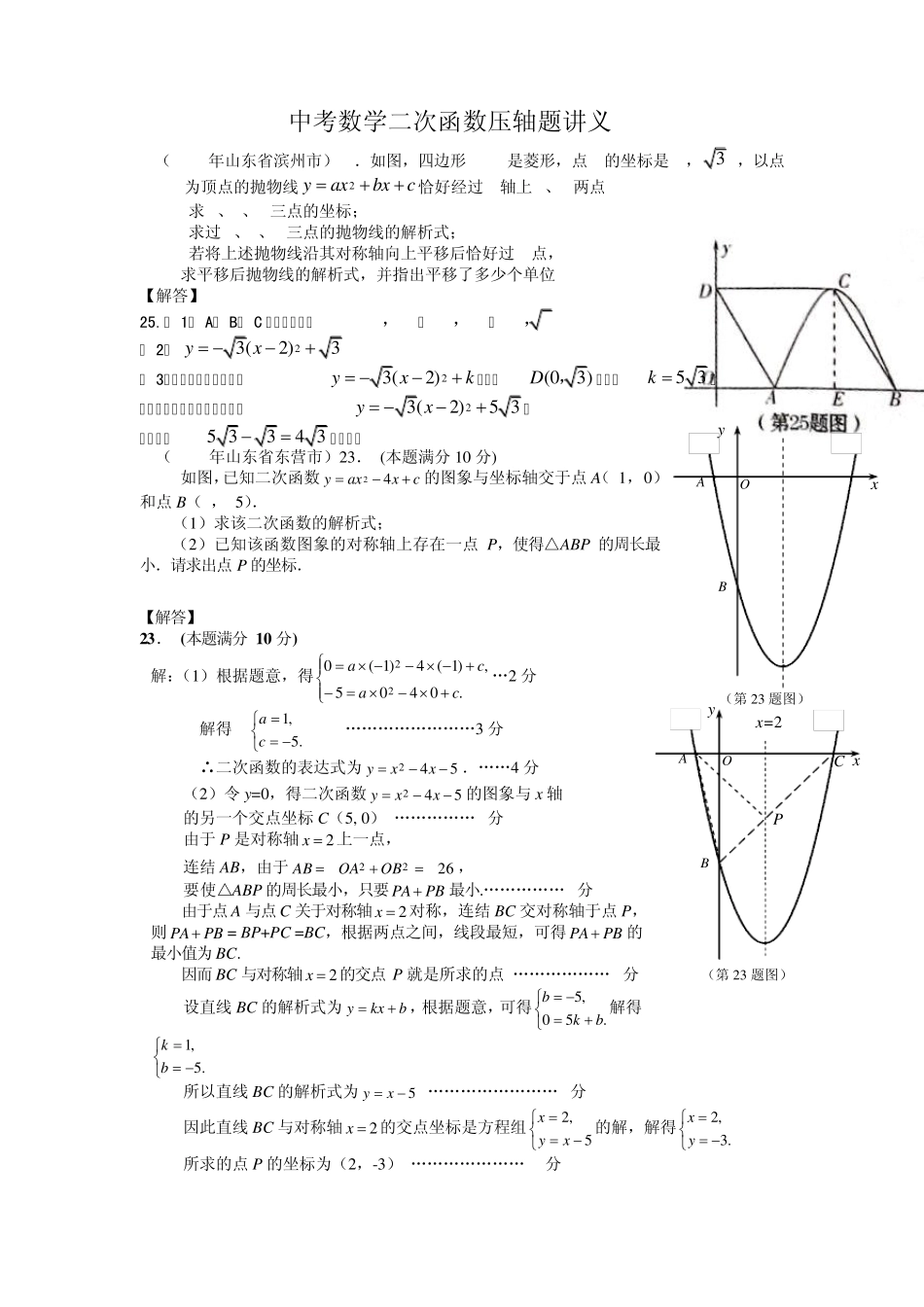
中考数学二次函数压轴题讲义 1.（2010年山东省滨州市）25．如图，四边形ABCD是菱形，点D的坐标是(0，3 )，以点C为顶点的抛物线 2yaxbxc恰好经过x轴上A、B两点 (1)求A、B、C三点的坐标； (2)求过A、B、C三点的抛物线的解析式； (3)若将上述抛物线沿其对称轴向上平移后恰好过D点， 求平移后抛物线的解析式，并指出平移了多少个单位? 【解答】 25.（ 1） A、 B、 C 的坐标分别为(1，0)， (3，0)， (2，3) （ 2）23(2)3yx  （ 3）设抛物线的解析式为23(2)yxk ，代入(03)D ，，可得5 3k ， ∴平移后的抛物线的解析式为23(2)5 3yx 。 ∴平移了5 334 3个单位。 2.（2010年山东省东营市）23． (本题满分10 分) 如图，已知二次函数24yaxxc的图象与坐标轴交于点A（-1， 0）和点B（0，-5）． （1）求该二次函数的解析式； （2）已知该函数图象的对称轴上存在一点P，使得△ABP 的周长最小．请求出点P 的坐标． 【解答】 23 ． (本题满分1 0 分) 解：（1）根据题意，得.0405,)1(4)1(022caca…2 分 解得 .5,1ca ……………………3 分 ∴二次函数的表达式为542xxy．……4 分 （2）令 y=0，得二次函数542xxy的图象与x 轴 的另一个交点坐标C（5, 0）.……………5分 由于P 是对称轴2x上一点， 连结 AB，由于2622OBOAAB， 要使△ABP 的周长最小，只要PBPA最小.……………6分 由于点A 与点C 关于对称轴2x对称，连结 BC 交对称轴于点P，则PBPA= BP+PC =BC，根据两点之间，线段最短，可得PBPA的最小值为BC. 因而 BC 与对称轴2x的交点P 就是所求的点.………………8分 设直线BC 的解析式为 bkxy，根据题意，可得.50,5bkb解得.5,1bk 所以直线BC 的解析式为5 xy.……………………9分 因此直线BC 与对称轴2x的交点坐标是方程组5,2xyx的解，解得.3,2yx 所求的点P 的坐标为（2，-3）.…………………10分 x O A （第 23 题图） B y x O A （第 23 题图） B y C P x=2 3.（2010年山东省德州市）23． (本题满分 11 分) 已知二次函数cbxaxy2的图象经过点 A(3，0)，B(2，-3)，C(0，-3)． (1)求此函数的解析式及图象的对称轴； (2)点 P 从 B 点出发以每秒 0.1...