中考数学二次函数压轴题题型归纳VIP免费

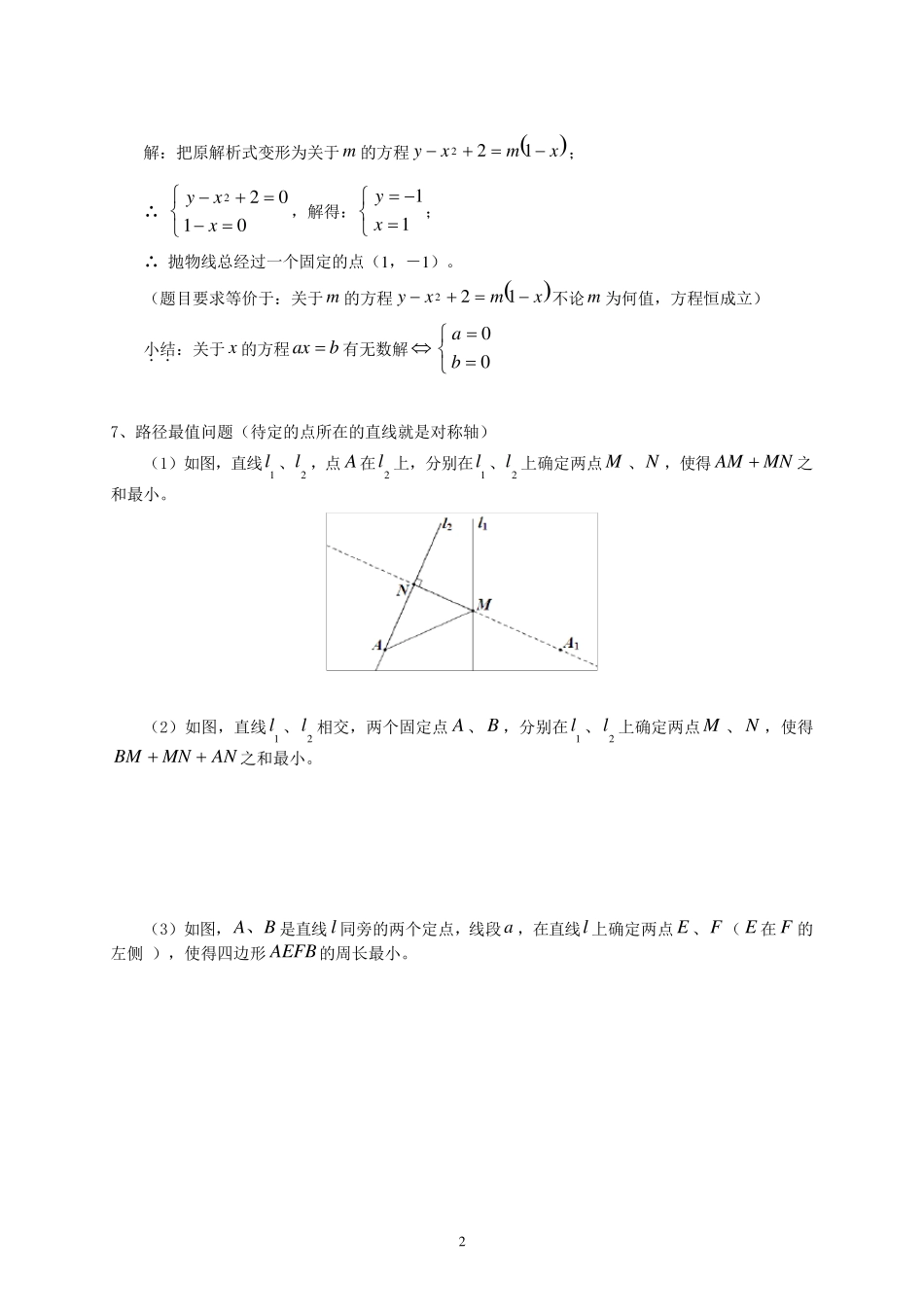
1 中考二次函数综合压轴题型归类 一、常考点汇总 1、两点间的距离公式： 22BABAxxyyAB 2、中点坐标：线段AB 的中点C 的坐标为：22BABAyyxx， 直线11bxky（01 k）与22bxky（02 k）的位置关系： （1）两直线平行21kk 且21bb  （2）两直线相交21kk  （3）两直线重合21kk 且21bb  （4）两直线垂直121kk 3、一元二次方程有整数根问题，解题步骤如下： ① 用 和参数的其他要求确定参数的取值范围； ② 解方程，求出方程的根；（两种形式：分式、二次根式） ③ 分析求解：若是分式，分母是分子的因数；若是二次根式，被开方式是完全平方式。 例：关于 x的一元二次方程01222＝－mxmx有两个整数根，5＜m且m 为整数，求m 的值。 4、二次函数与x轴的交点为整数点问题。（方法同上） 例：若抛物线3132xmmxy与x轴交于两个不同的整数点，且m 为正整数，试确定此抛物线的解析式。 5、方程总有固定根问题，可以通过解方程的方法求出该固定根。举例如下： 已知关于 x的方程23(1)230mxmxm（m 为实数），求证：无论m 为何值，方程总有一个固定的根。 解：当0m时，1x； 当0m时，032 m，mmx213，mx321、12 x； 综上所述：无论 m 为何值，方程总有一个固定的根是 1 。 6、函数过固定点问题，举例如下： 已知抛物线22mmxxy（m 是常数），求证：不论m 为何值，该抛物线总经过一个固定的点，并求出固定点的坐标。 2 解：把原解析式变形为关于m 的方程xmxy122； ∴ 01 02 2xxy，解得：1 1 xy； ∴ 抛物线总经过一个固定的点（1 ，－1 ）。 （题目要求等价于：关于m 的方程xmxy122不论 m 为何值，方程恒成立） 小结．．：关于x的方程bax有无数解0 0 ba 7、路径最值问题（待定的点所在的直线就是对称轴） （1）如图，直线1l 、2l ，点 A 在2l 上，分别在1l 、2l 上确定两点 M 、N ，使得MNAM 之和最小。 （2）如图，直线1l 、2l 相交，两个固定点 A 、 B ，分别在1l 、2l 上确定两点 M 、 N ，使得ANMNBM之和最小。 （3）如图，BA、是直线 l 同旁的两个定点，线段a ，在直线l 上确定两点 E 、F （ E 在 F 的左侧 ），使得四边形A...