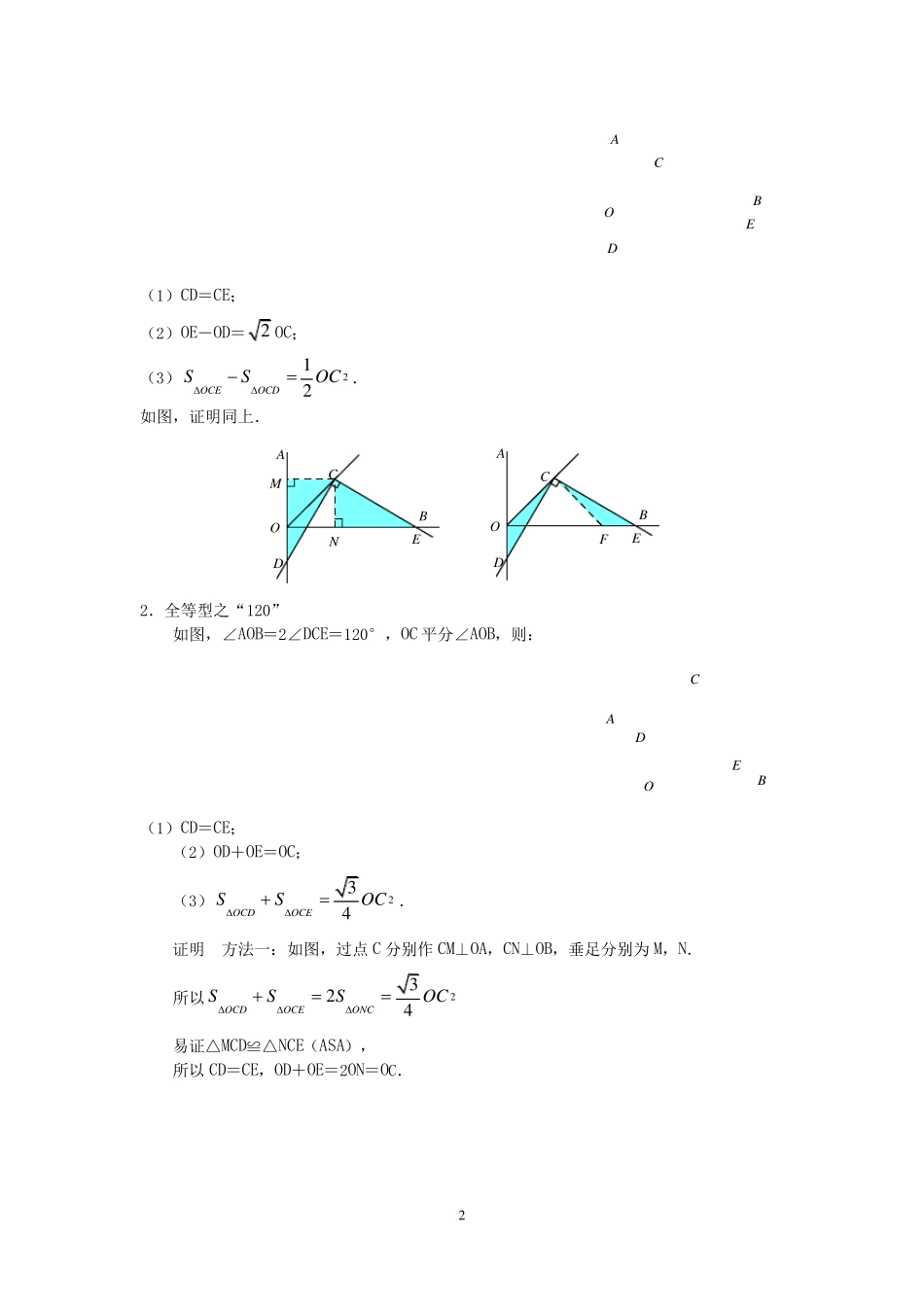
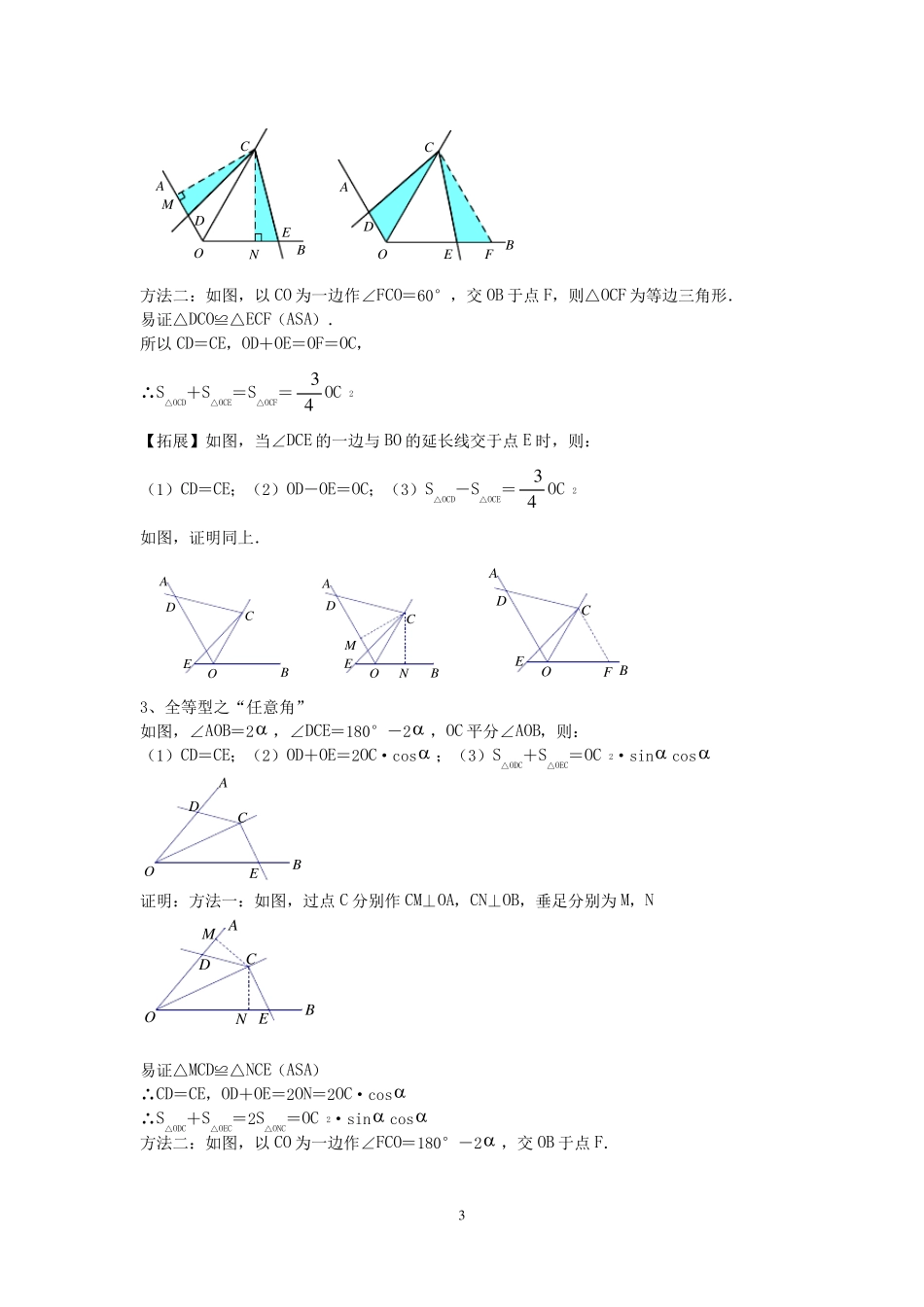
1 专题16《对角互补模型》 破解策略 1.全等型之“90°” 如图,∠AOB=∠DCE=90°,OC 平分∠AOB,则 AOBDCE (1)CD=CE; (2)OD+OE= 2 OC; (3)212OCDOCESSOC. 证明 方法一:如图,过点 C 分别作 CM⊥OA,CN⊥OB,垂足分别为 M,N. 由角平分线的性质可得 CM=CN,∠MCN=90°. 所以∠MCD=∠NCE, 从而△MCD≌△NCE(ASA), 故 CD=CE. 易证四边形 MONC为正方形. 所以 OD+OE=OD+ON+NE=2ON= 2 OC. 所以2212OCDOCEMONCSSSONOC正方形. 方法二:如图,过 C 作 CF⊥OC,交 OB 于点 F. 易证∠DOC=∠EFC=45°,CO=CF,∠DCO=∠ECF. 所以△DCO≌△ECF(ASA) 所以 CD=CE,OD=FE, 可得 OD+OE=OF=2 OC . 所以212OCDOCEOCFSSSOC. 【拓展】如图,当∠DCE 的一边与 AO 的延长线交于点 D 时,则: NMAOBDCEFAOBDCE2 BAECOD (1)CD=CE; (2)OE-OD=2 OC; (3)212OCEOCDSSOC. 如图,证明同上. FDOCEABNMDOCEAB 2.全等型之“120” 如图,∠AOB=2∠DCE=120°,OC 平分∠AOB,则: OBECDA (1)CD=CE; (2)OD+OE=OC; (3)234OCDOCESSOC. 证明 方法一:如图,过点 C 分别作 CM⊥OA,CN⊥OB,垂足分别为 M,N. 所以2324OCDOCEONCSSSOC 易证△MCD≌△NCE(ASA), 所以 CD=CE,OD+OE=2ON=OC. 3 NMADCEBOFADCEBO 方法二:如图,以CO 为一边作∠FCO=60°,交 OB 于点 F,则△OCF 为等边三角形. 易证△DCO≌△ECF(ASA). 所以CD=CE,OD+OE=OF=OC, ∴S△OCD+S△OCE=S△OCF=43 OC 2 【拓展】如图,当∠DCE 的一边与 BO 的延长线交于点 E 时,则: (1)CD=CE;(2)OD-OE=OC;(3)S△OCD-S△OCE=43 OC 2 如图,证明同上. EOBACD NMEOBACD FEOBACD 3、全等型之“任意角” 如图,∠AOB=2 ,∠DCE=180°-2 ,OC 平分∠AOB,则: (1)CD=CE;(2)OD+OE=2OC·cos ;(3)S△ODC+S△OEC=OC 2·sin cos EOBACD 证明:方法一:如图,过点 C 分别作CM⊥OA,CN⊥OB,垂足分别为M,N 易证△MCD≌△NCE(ASA) ∴CD=CE,OD+OE=2ON=2OC·cos ∴S△ODC+S△OEC=2S△ONC=OC 2·sin cos 方法二:如图,以CO 为一边作∠FCO=180°-2 ,交 OB 于点 F. MN EOBACD4 F...