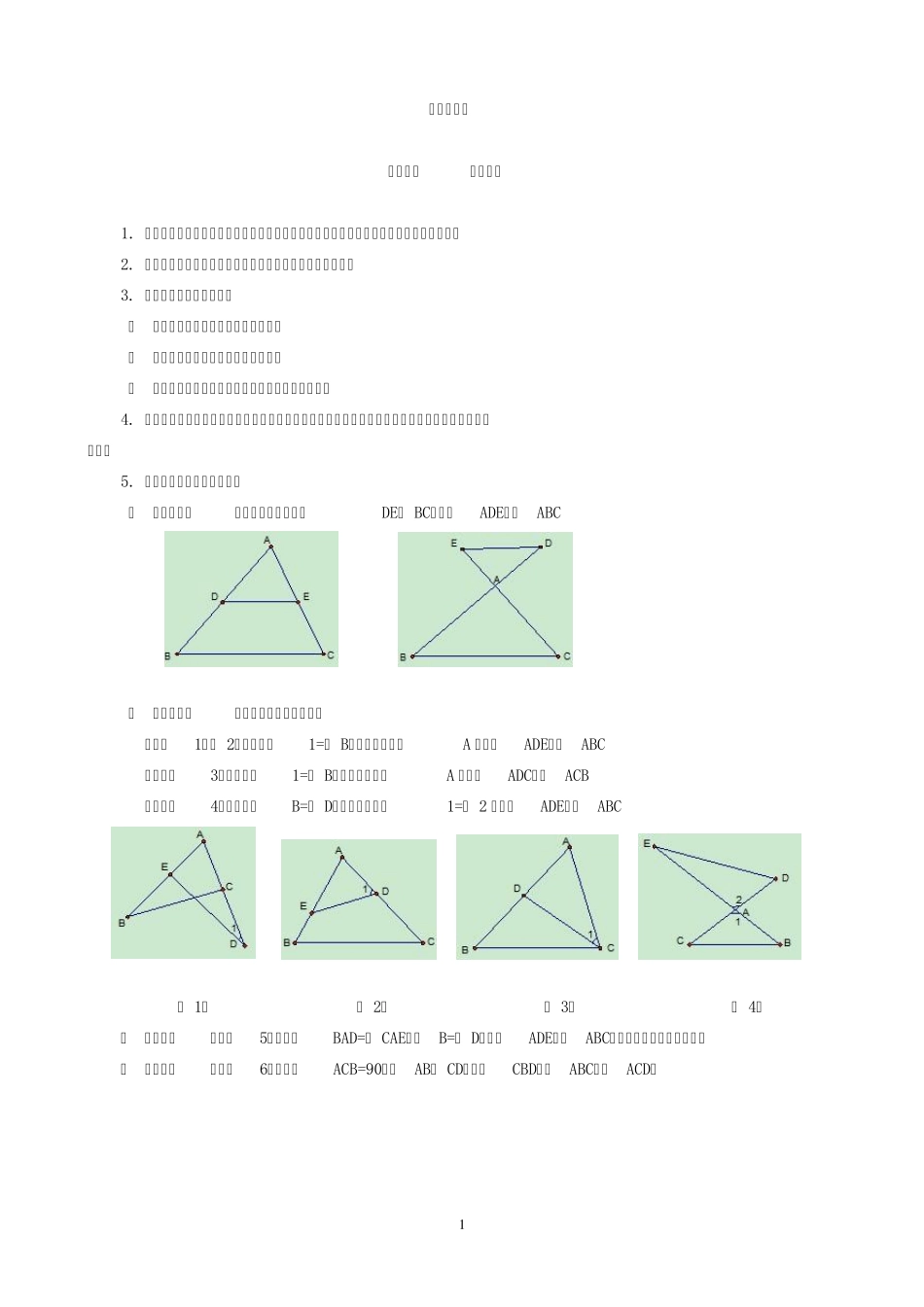
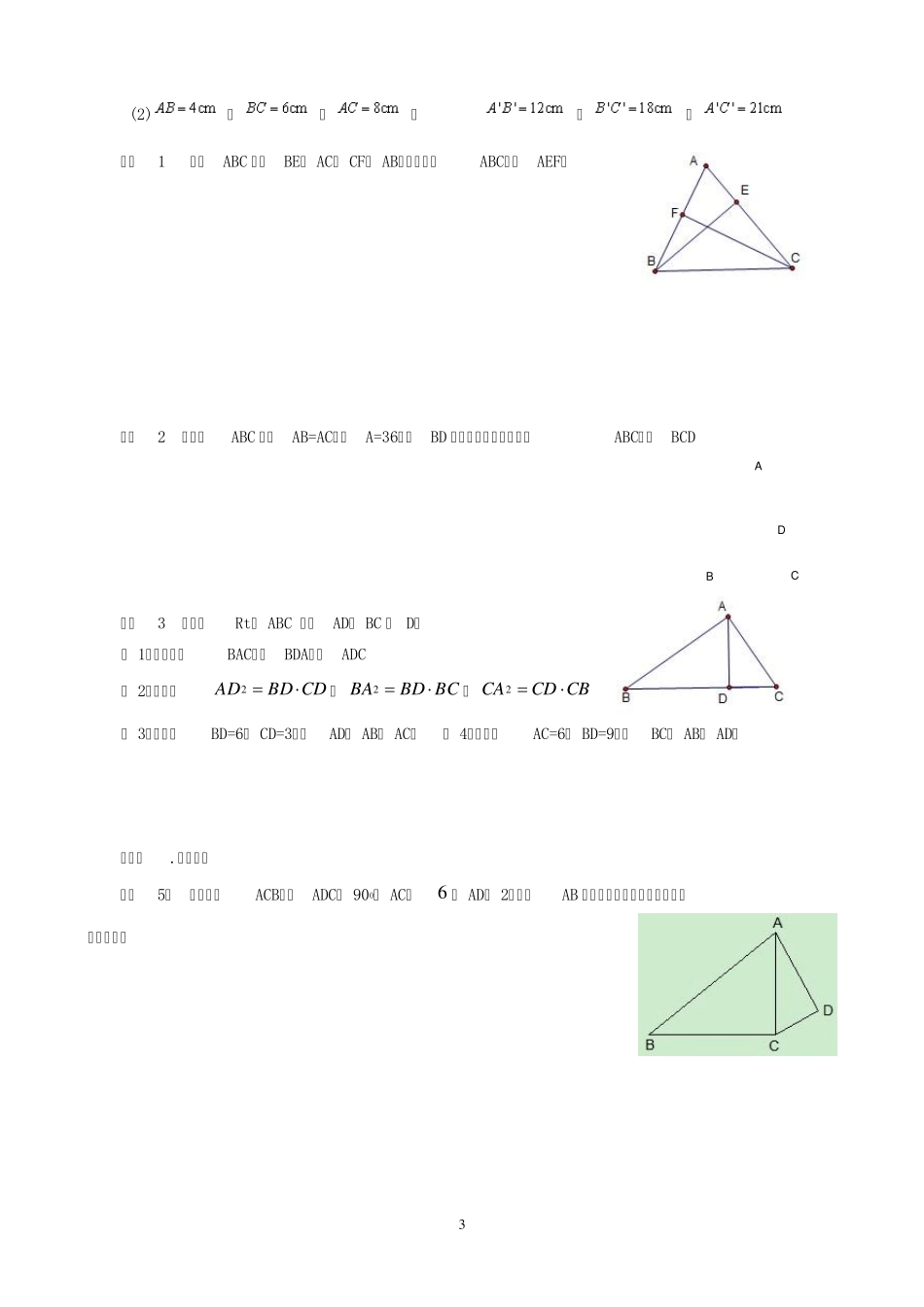
1 图形的相似 第一部分 知识梳理 1. 对应边成比例,对应角都相等的两个多边形相似。相似多边形的对应边之比叫做相似比。 2. 相似三角形:对应角相等,对应边成比例的两个三角形相似 3. 相似三角形的判定方法: ① 三边对应成比例的两个三角形相似。 ② 两个角对应相等的两个三角形相似。 ③ 两边对应成比例并且夹角相等的两个三角形相似。 4. 判定三角形相似,一般先找等角,当难发现等角或仅能判定一组等角时,则应转向证明边对应成比例。 5. 相似三角形几种基本类型: ① 平行线型:常见的有如下两种,DE∥ BC,则△ADE∽△ABC ② 相交线型:常见的有如下四种情形, 如图(1)( 2),已知∠1=∠ B,则由公共角∠A 得,△ADE∽△ABC 如下图(3),已知∠1=∠ B,则由公共角∠A 得,△ADC∽△ACB 如下图(4),已知∠B=∠ D,则由对顶角∠1=∠ 2 得,△ADE∽△ABC ( 1) ( 2) ( 3) ( 4) ③ 旋转型:如图(5)已知∠BAD=∠ CAE,∠B=∠ D,则△ADE∽△ABC,下图为常见的基本图形. ④ 母子型:如图(6)已知∠ACB=90°,AB⊥ CD,则△CBD∽△ABC∽△ACD. 2 BCADE ABCD ( 5) ( 6) 第二部分 精讲点拨 考点1.多边形相似 【例1】已知四边形ABCD 与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD 的周长为40,求四边形ABCD 的各边的长. 变式1 下列说法正确的是( ) A.所有的平行四边形都相似 B.所有的矩形都相似 C.所有的菱形都相似 D.所有的正方形都相似 变式2 如图,四边形ABCD 和 EFGH 相似,求角α 、 β 的大小和EH 的长度x。 考点2. 相似三角形 【例2】下列说法正确的是( ) A.全等三角形一定相似 B.相似三角形一定全等 C.有一个角是40°的两个等腰三角形相似 D.两个等腰直角三角形不一定相似 变式1 △ ABC 的三条边之比为2: 5: 6,与其相似的另一个△A′ B′ C′最大边长为15cm,则另两边长的和为 . 变式2 已知:在△ABC 中,三边长分别为2 ,1 0 , 2,△A’ B’ C’ 的两边长分别为1,5 ,若△ABC∽△A’ B’ C’,则△A’ B’ C’ 的第三边长为( ) A.22 B.2 C.2 D.22 考点3. 相似三角形的判定 【例3】根据下列条件,判断与是否相似,并说明里由: (1),,; ,, 3 (2),,; ,, 变式1 在△ABC 中,BE⊥ AC, CF⊥ AB,求证:△ABC∽△AEF...