杨辉三角和二项式系数的性质VIP免费

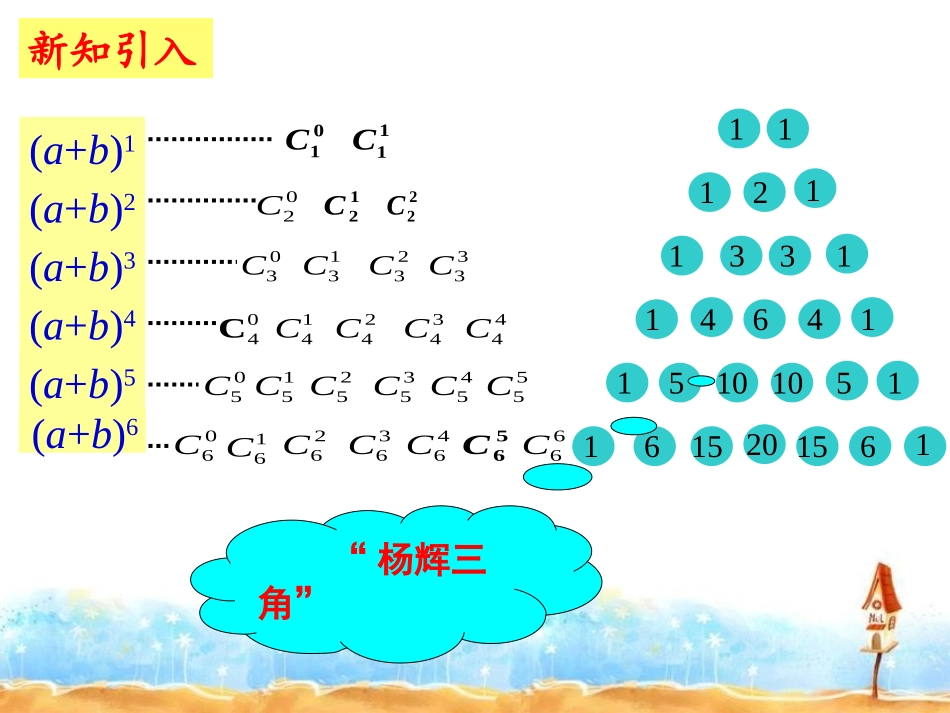
§1.3.2“§1.3.2“杨辉三角”与二项式系数的性质杨辉三角”与二项式系数的性质普通高中课程标准人教A版数学选修2-3复习回顾复习回顾二项式定理:011()()nnnknkknnnnnnabCaCabCabCbnN二项式系数(0,1,,)knCkn通项1knkkknTCab组合数两个性质:mnmnnCC11rrrnnnCCC01C02C12C22C03C13C23C33C14C04C34C24C44C05C15C25C35C45C55C66C36C46C56C26C16C06C11C11121133114641151010511615201561新知引入“杨辉三角”(a+b)1(a+b)2(a+b)3(a+b)4(a+b)5(a+b)6杨辉三角此表在我国南宋数学家杨辉1261年所著的《详解九章算法》里就已经出现，并且北宋数学家贾宪(约公元11世纪)已使用过它.杨辉(南宋)在欧洲，这个表被认为是法国数学家帕斯卡（1623-1662）首先发现的，他们把这个表叫做帕斯卡三角.杨辉三角的发现要比欧洲早五百年左右.十五一一一一一一一二十六六十五一一一一一一二三三四四六五十十五111211331146411510105116152015611101CC02C12C22C03C13C23C33C14C04C34C24C44C05C15C25C35C45C55C66C36C46C56C26C16C06Cn=6----n=5-------n=4----------对称性mnmnnCC11121133114641151010511615201561新知探究一:新知探究一:n=3--------------n=1------------------n=2----------------n=1------------------n=2----------------n=3--------------n=1---------------------n=2----------------1.对称性．与首末两端“等距离”的两个二项式系数相等.二项式系数的性质二项式系数的性质4+6=102+1=3例如：1112113311464115101051161520156121346101101CC02C12C22C03C13C23C33C14C04C34C24C44C05C15C25C35C45C55C66C36C46C56C26C16C06C新知探究二:新知探究二:173521135217纵向：相邻两行的数有什么关系？在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.（“双肩”和）122223CCC122445CCC11rrrnnnCCC1101CC02C12C22C03C13C23C33C14C04C34C24C44C05C15C25C35C45C55C66C36C56C16C06C11121133114641151010511615201561当n为偶数如2、4、6时，中间一项最大2.增减性与最大值新知探究三:新知探究三:1?kknnCC与的大小关系横向:每行系数大小变化趋势？当n为奇数如1、3、5时，中间两项最大n=6---n=5------n=4---------n=3------------n=1--------------------n=2---------------n=1--------------------n=2---------------n=3------------n=1--------------------n=2---------------n=6---n=5------n=4---------n=3------------n=1--------------------n=2---------------26C46C21nk可知，当时，二项式系数前半部分逐渐增大的，由对称性可知它的后半部分是逐渐减小的，且中间项取得最大值。增减性与最大值增减性与最大值1112nknkk1nkk1!!()!!(1)!(1)!knknnCknknCknk证明：（法一）21nk可知，当时，二项式系数前半部分逐渐增大的，由对称性可知它的后半部分是逐渐减小的，且中间项取得最大值。增减性与最大值增减性与最大值证明：（法二）!1!1!!!!1knknknknCCknkn111!!1!knkknkn2110111nkknkknk12345615101520ro()fr定义域为{0,1,2,…,n}.,()rnfrC其图象是7个孤立点.函数角度图象法图象法直线作为对称轴将图象分成对称的两部分2nr当n=6时,rCrf6nO2n2nOn当n是偶数时，中间的一一项取得最大值.2nnC当n是奇数时，中间的两项和相等,且同时取得最大值.12nnC12nnC2nr对称轴：n为奇数；如n=7n为偶数；如n=64336710203020156()fr()frrr21n21n新知探究四:新知探究四:012:.......2nnnnnnCCCC猜想248163264122252324262计算各行二项式系数的和，你能发现什么规律？11121133114641151010511615201561n=6---n=5----------n=4--------------n=3-------------------n=1----------------------------n=2-----------------------n01201122(1)=那么，？nrrnnnnnnnnnnnnCCCCCCxxCxCxCx0121,2令则nnnnnnxCCCC3....