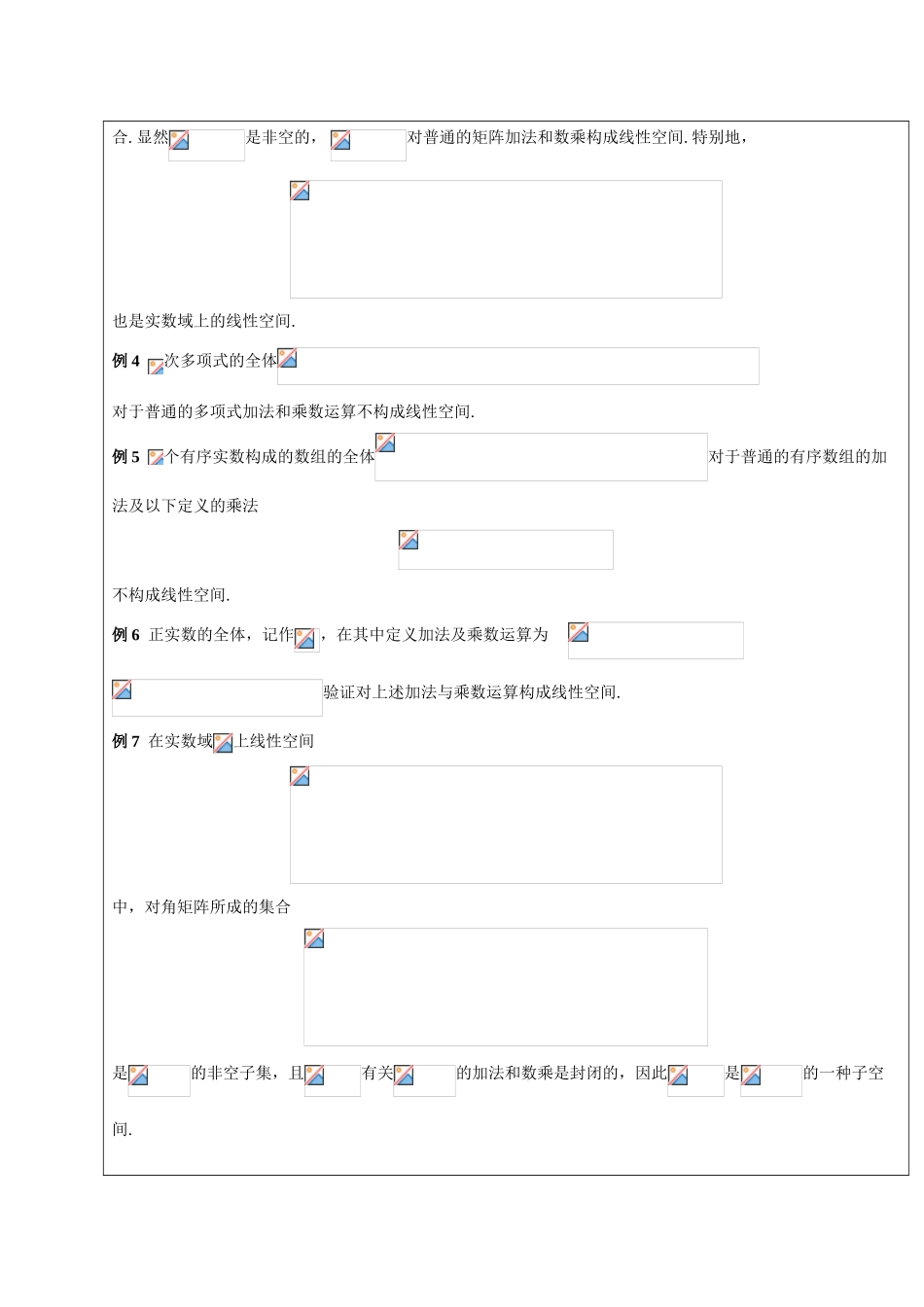
线性代数教学教案第五章 线性空间与线性变换授课序号 01教 学 基 本 指 标教学课题第五章 第一节 线性空间的定义与性质课的类型新知识课教学办法讲授、课堂提问、讨论、启发、自学教学手段黑板多媒体结合教学重点线性空间与子空间的概念、线性空间的性质教学难点线性空间、子空间的鉴定参考教材同济版《线性代数》作业布置课后习题大纲规定理解线性空间和子空间的概念;理解线性空间的性质。教 学 基 本 内 容一、 线性空间的定义:定义 1:设是一种非空集合,为实数域. 对于任意两个元素,在中总有唯一拟定的一种元素与之对应,称为与的和,记作. 对于中任一数与中任一元素,在中总有唯一拟定的一种元素与之对应,称为与的数量乘积,记作.如果这两种运算满足下列八条运算规律(设):(i) 加法交换律:;(ii) 加法结合律: ;(iii) 在中存在零元素;对于任何,都有是;(iv) 负元素:对于任何,都有是的负元素,使;(v) ;(vi) ;(vii) ;(viii) ;那么,就称为实数域上的线性空间. 二、线性空间的性质:性质 1 零元素是唯一的.性质 2 任一元素的负元素是唯一的(后来 将的负元素记作).性质 3 .性质 4 如果,则或.三、线性空间的子空间:定义 2:设是实数域上线性空间,是的一种非空子集. 如果有关的加法和数乘运算也构成线性空间,则称是的一种子空间.定理 实数域上线性空间的非空子集成为的一种子空间的充足必要条件是有关的加法和数乘是封闭的.四、重要例题:例 1 次数不超出的多项式的全体,记作,即,对于普通的多项式加法、数乘多项式的乘法构成线性空间. 例 2 设集合是定义在区间上的持续实函数全体所成的集合,有关普通的函数加法和数乘函数的乘法构成线性空间. 例 3 设是实数域上的矩阵全体所成的集合. 显然是非空的, 对普通的矩阵加法和数乘构成线性空间. 特别地,也是实数域上的线性空间.例 4 次多项式的全体对于普通的多项式加法和乘数运算不构成线性空间. 例 5 个有序实数构成的数组的全体对于普通的有序数组的加法及以下定义的乘法不构成线性空间.例 6 正实数的全体,记作,在其中定义加法及乘数运算为验证对上述加法与乘数运算构成线性空间.例 7 在实数域上线性空间中,对角矩阵所成的集合是的非空子集,且有关的加法和数乘是封闭的,因此是的一种子空间.授课序号 02教 学 基 本 指 标教学课题第五章 第二节 维数、基与坐标课的类型新知识课教学办法讲授、课堂...