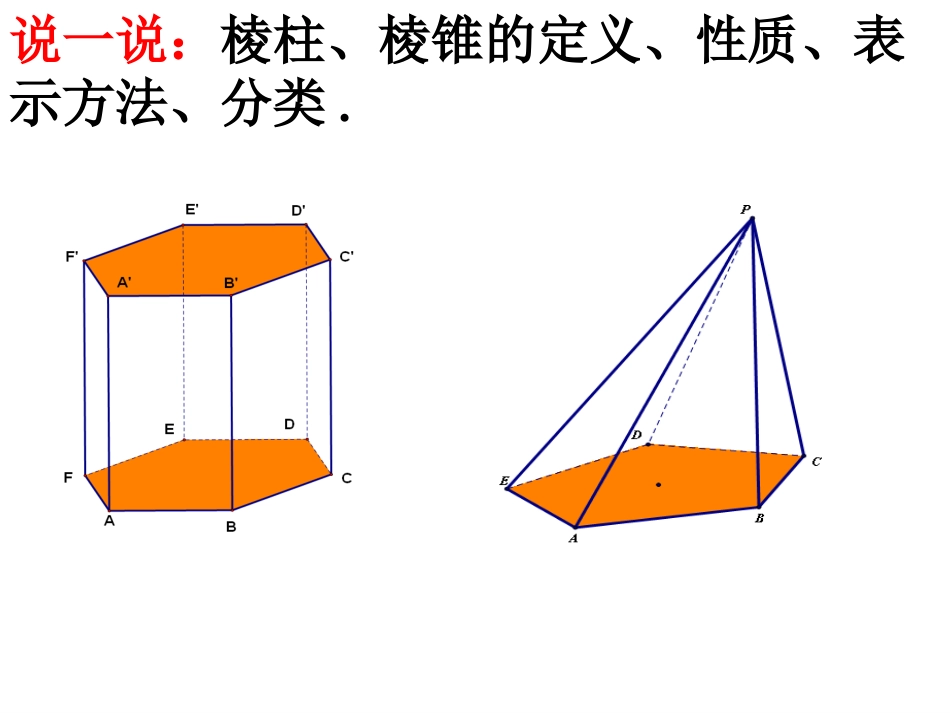
说一说:棱柱、棱锥的定义、性质、表示方法、分类.多面体(polyhedron):由若干个平面多边形围成的几何体多面体有几个面就称为几面体,如三棱锥是四面体思考:多面体至少有几个面?这个多面体是怎样的几何体?棱柱、棱锥、棱台都是由一些平面多边形围成的几何体。四个面、三棱锥或者四面体实例知识探究(一):圆柱的结构特征思考1:如图所示的空间几何体叫做圆柱,那么圆柱是怎样形成的呢?以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的曲面所围成的几何体.思考2:结合图形正确理解概念侧面轴母线底面母线知识探究(二):圆锥的结构特征思考1:如图所示的空间几何体叫做圆锥,圆锥是由什么平面图形旋转一周形成的?侧面顶点母线底面母线轴思考2:结合图形正确理解概念思考1:用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分叫做圆台.圆台可以由什么平面图形旋转一周而形成?知识探究(三):圆台的结构特征思考2:与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线,它们的含义分别如何?侧面上底面下底面母线轴思考3:经过圆柱的轴的截面称为轴截面,你能说出圆柱的轴截面有哪些基本特征吗?思考3:经过圆锥任意两条母线的截面是什么图形?思考4:经过圆锥的轴的截面称为轴截面,你能说出圆锥的轴截面有哪些基本特征吗?思考3:经过圆台任意两条母线的截面是什么图形?轴截面有哪些基本特征?圆柱、圆锥、圆台名称圆柱圆锥圆台图形定义性质以矩形一边所在直线为轴,其余各边旋转一周而成的曲面所围成的几何体。以直角三角形一直角边所在直线为轴,其余各边旋转一周而成的曲面所围成的几何体以直角梯形垂直于底边的腰所在直线为轴,其余各边旋转一周而成的曲面所围成的几何体轴截面是全等的矩形轴截面是全等的等腰三角形轴截面是全等的等腰梯形hlrlhRrhlroo’sooo’O半径球心半圆绕着它的直径所在直线旋转一周而形成的面叫做球面,球面所围成的几何体叫做球体,简称球.知识探究(四):球的结构特征旋转体一般地,一条平面曲线绕它所在的平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体称为旋转体。圆柱、圆锥、圆台和球都是特殊的旋转体。母线圆锥面母线圆柱面母线旋转轴旋转面更多旋转体在生产和生活中,还有哪些几何体具有类似的生成规律?几何体的分类几何体的分类柱体锥体台体球多面体旋转体知识小结知识小结简单几何体的结构特征柱体锥体台体球棱柱圆柱棱锥圆锥棱台圆台AB图1AB图2AB图3例1将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?理论迁移