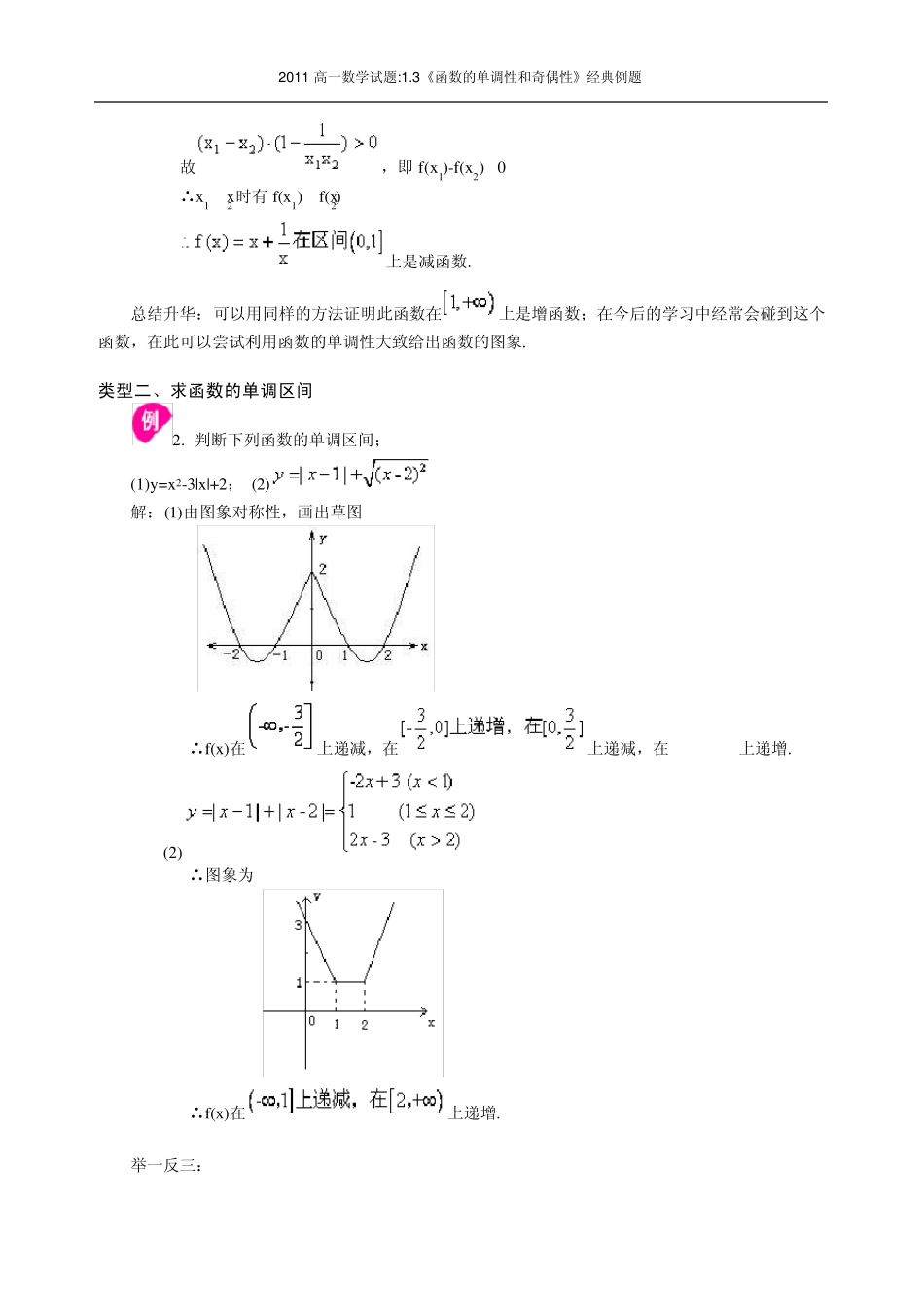
2011 高一数学试题:1.3《函数的单调性和奇偶性》经典例题 经典例题透析 类型一、函数的单调性的证明 1.证明函数上的单调性. 证明:在(0,+∞)上任取 x 1、x2(x 1≠x2), 令△x =x 2-x 1>0 则 x 1>0,x 2>0,∴ ∴上式<0,∴△y =f(x 2)-f(x 1)<0 ∴上递减. 总结升华: [1]证明函数单调性要求使用定义; [2]如何比较两个量的大小?(作差) [3]如何判断一个式子的符号?(对差适当变形) 举一反三: 【变式 1】用定义证明函数上是减函数. 思路点拨:本题考查对单调性定义的理解,在现阶段,定义是证明单调性的唯一途径. 证明:设 x1,x 2 是区间上的任意实数,且 x 10 ∴x1f(x2) 上是减函数. 总结升华:可以用同样的方法证明此函数在上是增函数;在今后的学习中经常会碰到这个函数,在此可以尝试利用函数的单调性大致给出函数的图象. 类型二、求函数的单调区间 2. 判断下列函数的单调区间; (1)y=x2-3|x|+2; (2) 解:(1)由图象对称性,画出草图 ∴f(x)在上递减,在上递减,在上递增. (2) ∴图象为 ∴f(x)在上递增. 举一反三: 2011 高一数学试题:1.3《函数的单调性和奇偶性》经典例题 【变式1】求下列函数的单调区间: (1)y=|x+1|; (2) (3). 解:(1)画出函数图象, ∴函数的减区间为,函数的增区间为(-1,+∞); (2)定义域为, 其中u=2x-1 为增函数, 在(-∞,0)与(0,+∞)为减函数,则上为减函数; (3)定义域为(-∞,0)∪(0,+∞), 单调增区间为:(-∞,0),单调减区间为(0,+∞). 总结升华: [1]数形结合利用图象判断函数单调区间; [2]关于二次函数单调区间问题,单调性变化的点与对称轴相关. [3]复合函数的单调性分析:先求函数的定义域;再将复合函数分解为内、外层函数;利用已知函数的单调性解决.关注:内外层函数同向变化→复合函数为增函数;内外层函数反向变化→复合函数为减函数. 类型三、单调性的应用(比较函数值的大小,求函数值域,求函数的最大值或最小值) 3. 已知函数f(x)在(0,+∞)上是减函数,比较 f(a2-a+1)与的大小. 解: 又 f(x)在(0,+∞)上是减函数,则. 4. 求下列函数值域: (1); 1)x∈[5,10]; 2)x∈(-3,-2)∪(-2,1); (2)y=x2-2x+3; 1)x∈[-1,1]; 2)x∈[-2,2...