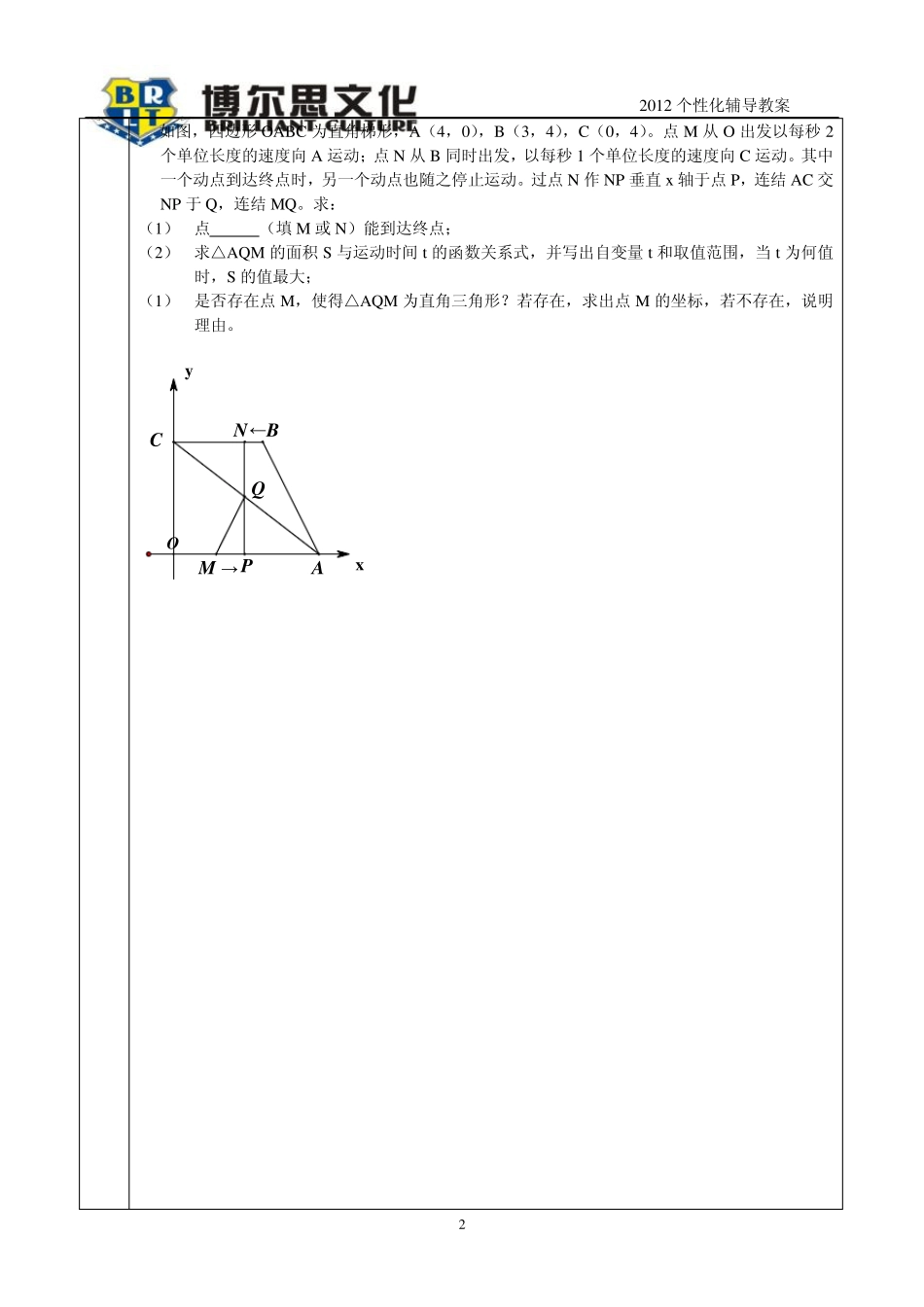
2012 个性化辅导教案 1 老师 姓名 学生姓名 学管师 学科 名称 年级 上课时间 月 日 _ _ :00-- _ _ :00 课题 名称 直角三角形的存在问题 教学 重点 教 学 过 程 【经典练习讲解】 1. (2011•济南)如图,矩形OABC 中,点O 为原点,点A 的坐标为(0,8),点C 的坐标为(6,0).抛物线y=﹣x2+bx+c 经过A、C 两点,与AB 边交于点D. (1)求抛物线的函数表达式; (2)点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ 的面积为S. ①求S 关于m 的函数表达式,并求出 m 为何值时,S 取得最大值; ②当 S 最大时,在抛物线y=﹣x2+bx+c 的对称轴 l 上若存在点F,使△FDQ 为直角三角形,请直接写出所有符合条件的F 的坐标;若不存在,请说明理由. 2012 个性化辅导教案 2 2. 如图,四边形OABC 为直角梯形,A(4,0),B(3,4),C(0,4)。点M 从O 出发以每秒2个单位长度的速度向A 运动;点N 从B 同时出发,以每秒1 个单位长度的速度向C 运动。其中一个动点到达终点时,另一个动点也随之停止运动。过点N 作NP 垂直x 轴于点P,连结AC 交NP 于Q,连结MQ。求: (1) 点 (填M 或N)能到达终点; (2) 求△AQM 的面积 S 与运动时间 t 的函数关系式,并写出自变量 t 和取值范围,当 t 为何值时,S 的值最大; (1) 是否存在点M,使得△AQM 为直角三角形?若存在,求出点M 的坐标,若不存在,说明理由。 ←→yxOQBCANPM 2012 个性化辅导教案 3 3. (2010•铜仁地区)如图所示,矩形OABC 位于平面直角坐标系中,AB=2,OA=3,点P 是OA上的任意一点,PB 平分∠APD,PE 平分∠OPF,且 PD、PF 重合. (1)设 OP=x,OE=y,求 y 关于x 的函数解析式,并求 x 为何值时,y 的最大值; (2)当 PD⊥OA 时,求经过 E、P、B 三点的抛物线的解析式; (3)请探究:在(2)的条件下,抛物线上是否存在一点M,使得△EPM 为直角三角形?若存在,求出 M 点的坐标;若不存在,请说明理由. 4. (2011•潼南县)如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线 y=x2+bx+c 经过 A,B 两点,抛物线的顶点为 D. 2012 个性化辅导教案 4 (1)求b,c 的值; (2)点E 是直角三角形ABC 斜边AB 上一动点(点A、B 除外),过点E 作x ...