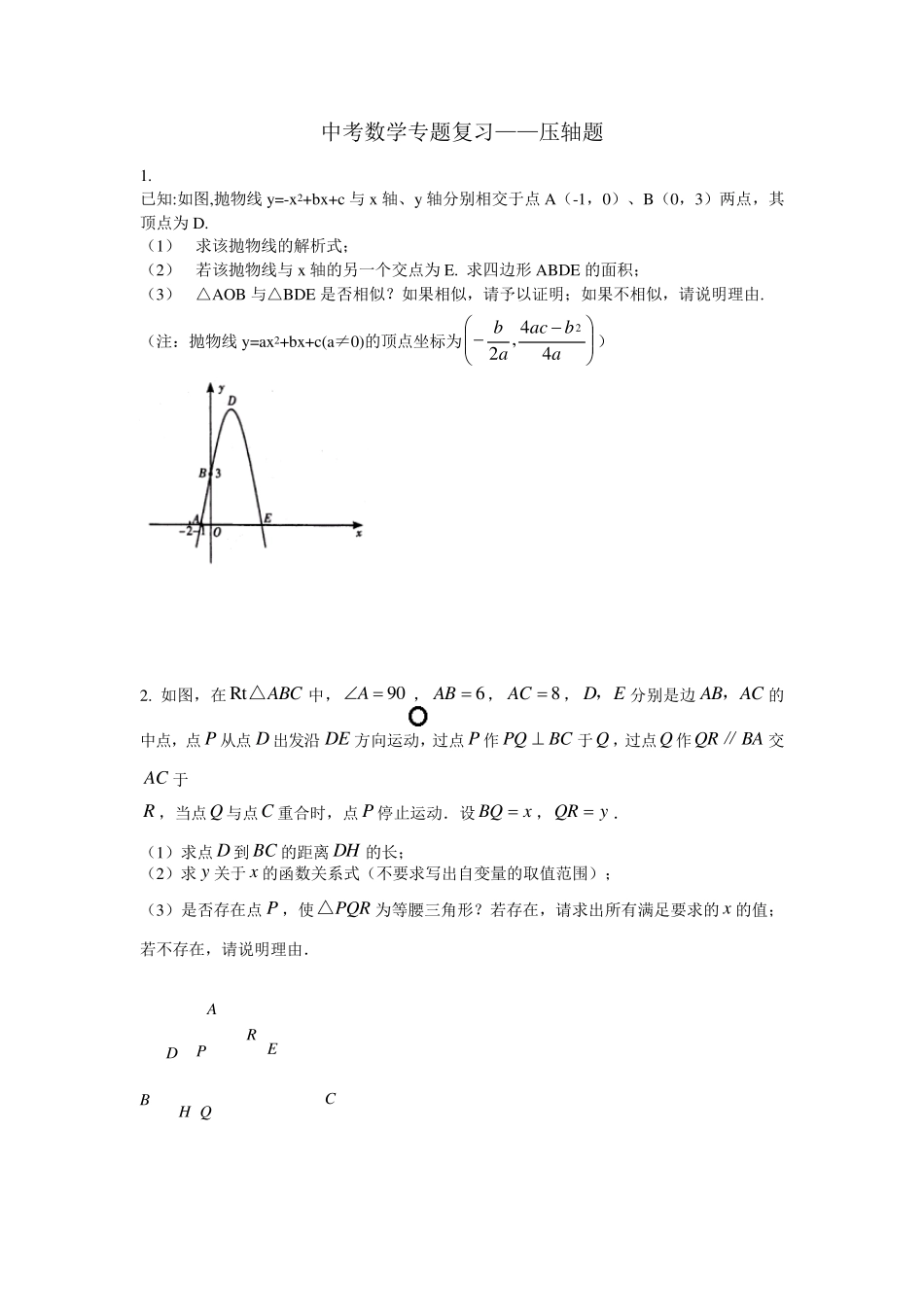
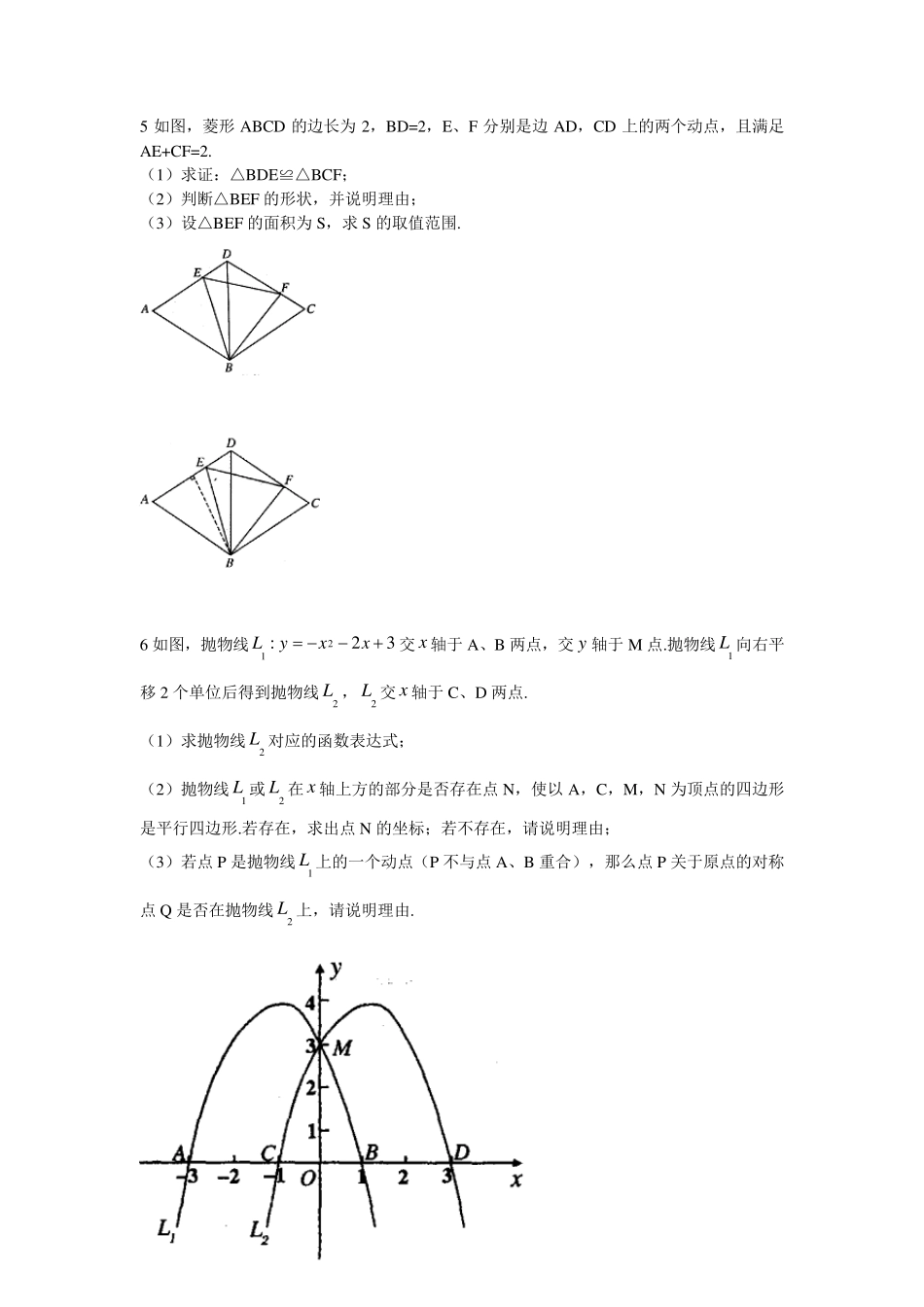
中考数学专题复习——压轴题 1. 已知:如图,抛物线 y =-x 2+bx +c 与 x 轴、y 轴分别相交于点 A(-1,0)、B(0,3)两点,其顶点为 D. (1) 求该抛物线的解析式; (2) 若该抛物线与 x 轴的另一个交点为 E. 求四边形 ABDE 的面积; (3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线 y =ax 2+bx +c(a≠0)的顶点坐标为abacab44,22) 2. 如图,在 RtABC△中,90A,6AB ,8AC , DE,分别是边 ABAC,的中点,点 P 从点 D 出发沿 DE 方向运动,过点 P 作 PQBC于Q ,过点Q 作QRBA∥交AC 于 R ,当点Q 与点C 重合时,点 P 停止运动.设 BQx,QRy. (1)求点 D 到 BC 的距离 DH 的长; (2)求 y 关于 x 的函数关系式(不要求写出自变量的取值范围); (3)是否存在点 P ,使PQR△为等腰三角形?若存在,请求出所有满足要求的 x 的值;若不存在,请说明理由. A B C D E R P H Q 3 在△ABC 中,∠A=90°,AB=4,AC=3,M 是 AB 上的动点(不与 A,B 重合),过 M点作 MN∥BC 交 AC 于点 N.以 MN 为直径作⊙O,并在⊙O 内作内接矩形 AMPN.令 AM=x. (1)用含 x 的代数式表示△MNP 的面积 S; (2)当 x 为何值时,⊙O 与直线 BC 相切? (3)在动点 M 的运动过程中,记△MNP 与梯形 BCNM 重合的面积为 y,试求 y 关于 x的函数表达式,并求 x 为何值时,y 的值最大,最大值是多少? 4.如图 1,在平面直角坐标系中,己知Δ AOB是等边三角形,点 A的坐标是 (0,4),点B在第一象限,点 P是x轴上的一个动点,连结AP,并把 Δ AOP绕着点 A按逆时针方向旋转 .使边 AO与AB重合 .得到 Δ ABD.(1)求直线 AB的解析式;( 2)当点 P运动到点(3 ,0)时,求此时 DP的长及点 D的坐标;( 3)是否存在点 P,使 Δ OPD的面积等于 43,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. A B C M N P 图 3 O A B C M N D 图 2 O A B C M N P 图 1 O 5 如图,菱形ABCD 的边长为2,BD=2,E、F 分别是边AD,CD 上的两个动点,且满足AE+CF=2. (1)求证:△BDE≌△BCF; (2)判断△BEF 的形状,并说明理由; (3)设△BEF 的面积为S,求S的取值范围. 6 如图,抛物线21...