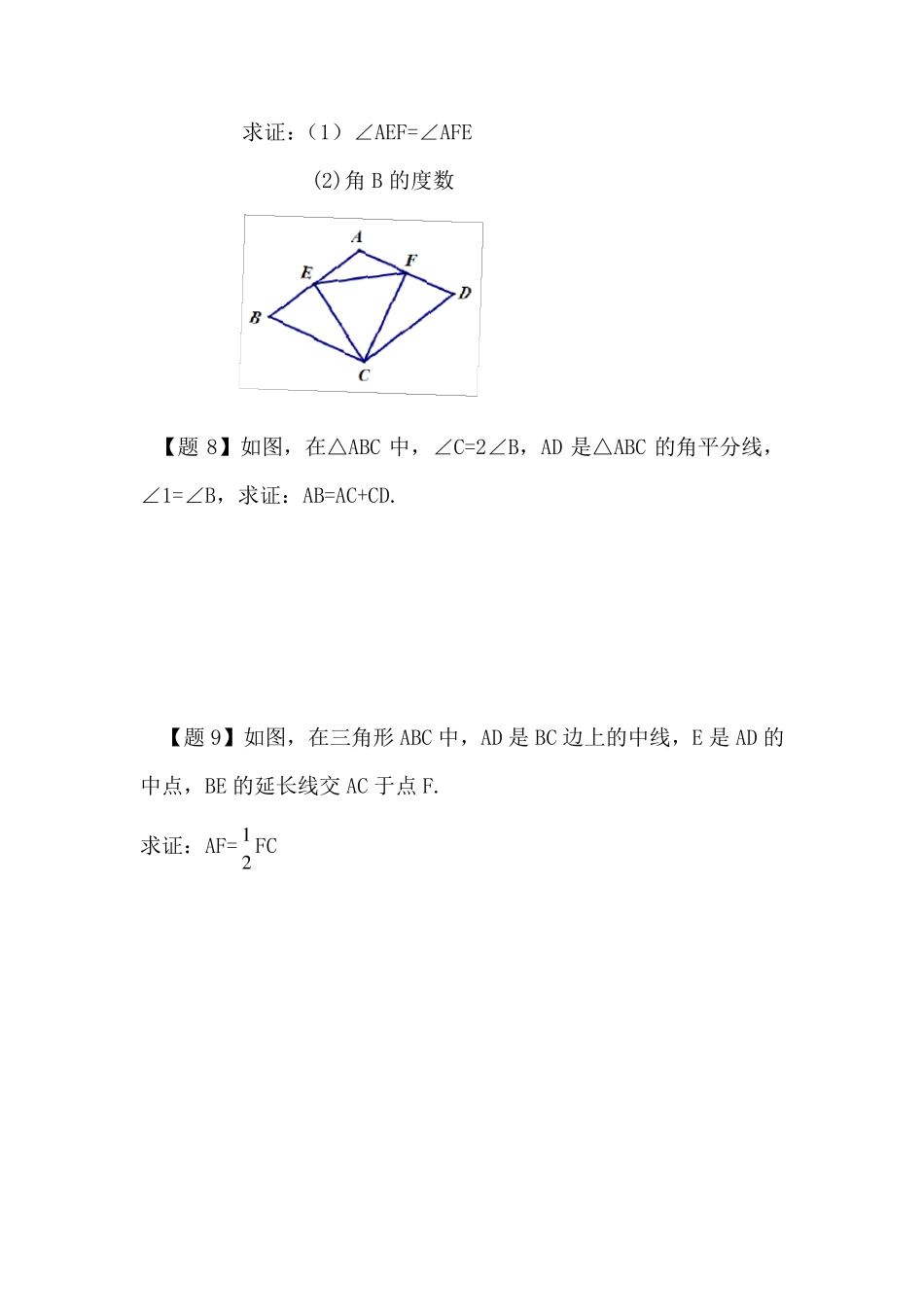
几何证明 【知识要点】 1.进一步掌握直角三角形的性质,并能够熟练应用; 2.通过本节课的学习能够熟练地写出较难证明的求证; 3.证明要合乎逻辑,能够应用综合法熟练地证明几何命题。 【概念回顾】 1.全等三角形的性质:对应边( ),对应角( )对应高线( ),对应中线( ),对应角的角平分线( )。 2.在Rt△ABC 中,∠C=90°,∠A=30°,则 BC:AC:AB=( )。 【例题解析】 【题1】已知在ΔABC 中,108A ,AB=AC,BD 平分ABC.求证:BC=AB+CD. 【题2】如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF. 【题3】如图,AD 为ΔABC 的角平分线且BD=CD.求证:AB=AC. ECDGABBDACFE 【题4】已知:如图,点B、F、C、E 在同一直线上,BF=CE,AB∥ED,AC∥FD,证明AB=DE,AC=DF. 【题5】已知:如图,△ABC 是正三角形,P 是三角形内一点,PA=3,PB=4,PC=5. 求:∠APB 的度数. 【题6】如图:△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过 C 作 CF⊥AE,垂足是F,过 B 作 BD⊥BC 交 CF 的延长线于 D。 (1) 求证:AE=CD; (2) 若 AC=12 ㎝,求BD 的长. 【题7】等边三角形CEF 于菱形ABCD 边长相等. A P C B 求证:(1)∠AEF=∠AFE (2)角 B 的度数 【题 8】如图,在△ABC 中,∠C=2∠B,AD 是△ABC 的角平分线,∠1=∠B,求证:AB=AC+CD. 【题 9】如图,在三角形 ABC 中,AD 是 BC 边上的中线,E 是 AD 的中点,BE 的延长线交 AC 于点 F. 求证:AF=21 FC 【题10】如图,将边长为1的正方形ABCD 绕点C 旋转到A'B'CD'的位置,若∠B'CB=30度,求AE 的长. 【题1 1 】AD,BE 分别是等边△ABC 中BC,AC 上的高。M,N 分别在AD,BE的延长线上,∠CBM=∠ACN.求证AM=BN. 【题12】已知:如图,AD、BC 相交于点O,OA=OD,OB=OC,点E、F 在AD 上,且AE=DF,∠ABE=∠DCF. 求证:BE‖CF. OFEDCBA 【巩固练习】 【练1】 如图,已知BE 垂直于AD,CF 垂直于AD,且BE=CF. (1)请你判断AD 是三角形ABC 的中线还是角平分线?请证明你的结论。 (2)链接 BF,CE,若四边形BFCE 是菱形,则三角形ABC 中应添加一个什么条件? 【练2】在等腰直角三角形ABC 中,O 是斜边 AC 的中点,P 是斜边上的一个动点,且PB=PD,DE 垂直AC,垂足为 E。 (1)求证:PE=BO (2)...