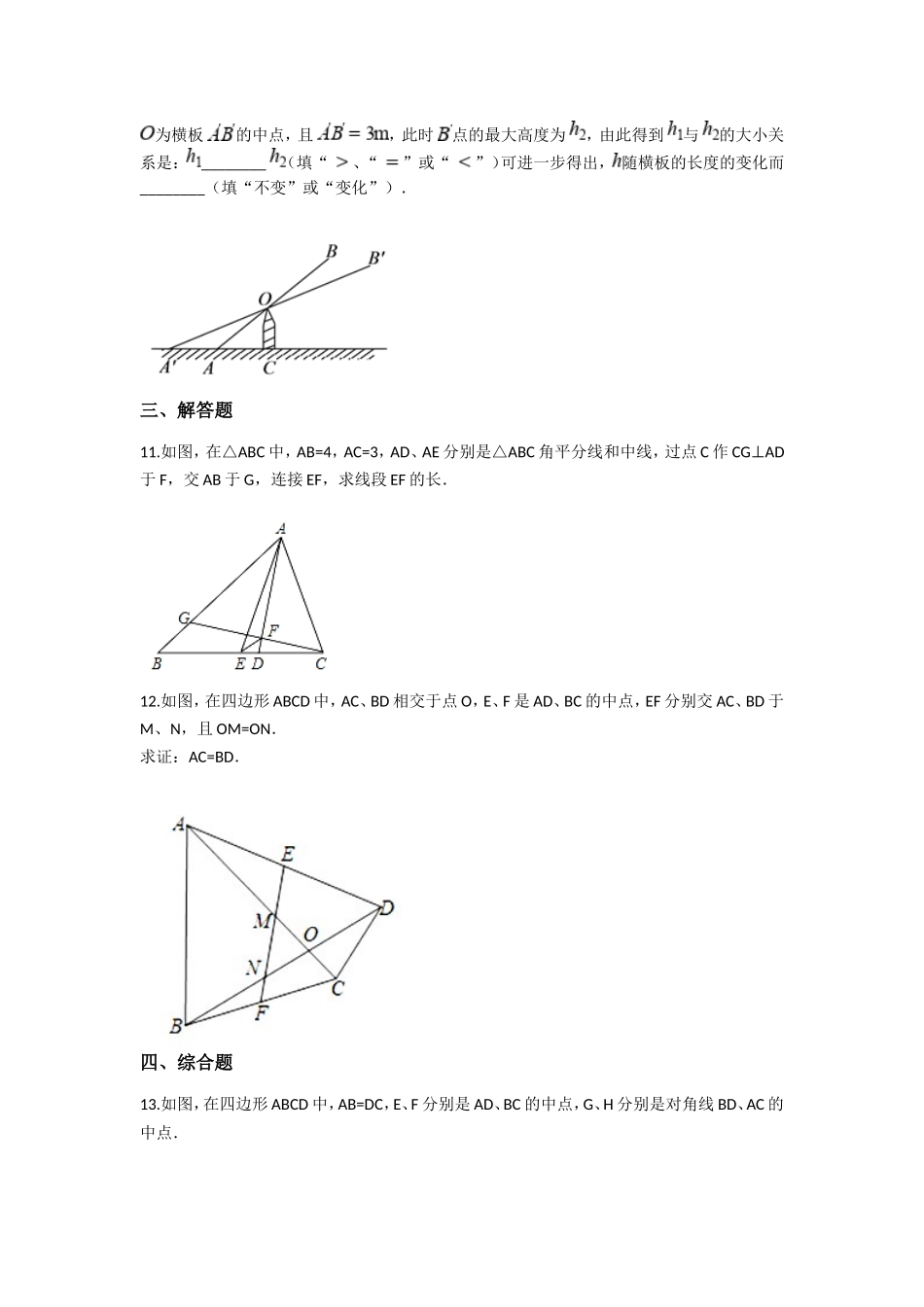
中考数学专项练习-三角形的中位线定理(含解析)一、单选题1.如图,为测量池塘边上两点 A,B 之间的距离,能够在池塘的一侧选用一点 O,连接 OA,OB,并分别取它们的中点 D,E,连接 DE,现测出 AO=36 米,BO=30 米,DE=20 米,那么 A,B 间的距离是( ) A. 30 米 B. 40 米 C. 60 米 D. 72 米2.如图,点 D,E,F 分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( ) A. AD 平分∠BAC B. EF=BC C. EF 与 AD 互相平分 D. DFE△是△ABC 的位似图形3.如图,在△ABC 中,BC=6,M、N 分别是 AB、AC 的中点,则 MN 等于( )A. 12 B. 6 C. 3 D. 4.如图,在△ABC 中,D,E 分别是 AB,AC 的中点,AC=12,F 是 DE 上一点,连接 AF,CF,DF=1.若∠AFC=90°,则 BC 的长度为( )A. 12 B. 13 C. 14 D. 155.已知△ABC 的各边长度分别为 3cm,4cm,5cm,则连结各边中点的三角形的周长为( ) A. 2cm B. 7cm C. 5cm D. 6cm6.已知△ABC 的周长为 50cm,中位线 DE=8cm,中位线 EF=10cm,则另一条中位线 DF 的长是( ) A. 5cm B. 7cm C. 9cm D. 10cm二、填空题7.如图,已知△ABC 中,AB=AC,AD 平分∠BAC,E 是 AB 的中点,若 AC=6,则 DE 的长为 ________8.如图,在△ABC 中,若 E 是 AB 的中点,F 是 AC 的中点,∠B=50°,则∠AEF=________. 9.如图,为预计池塘两岸边 A,B 两点间的距离,在池塘的一侧选用点 O,分别取 OA、OB 的中点 M,N,测得 MN=39m,则 A,B 两点间的距离是________ m. 10.如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 与否会随横板长度的变化而变化呢?一位同窗做了以下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: ________ (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而________(填“不变”或“变化”).三、解答题11.如图,在△ABC 中,AB=4,AC=3,AD、AE 分别是△ABC 角平分线和中线,过点 C 作 CGAD⊥于 F,交 AB 于 G,连接 EF,求线段 EF 的长.12.如图,在四边形 ABCD 中,AC、BD 相交于点 O,E、F 是 AD、BC 的中点,EF 分别交 AC、BD 于M、N,且 OM=ON.求证:A...