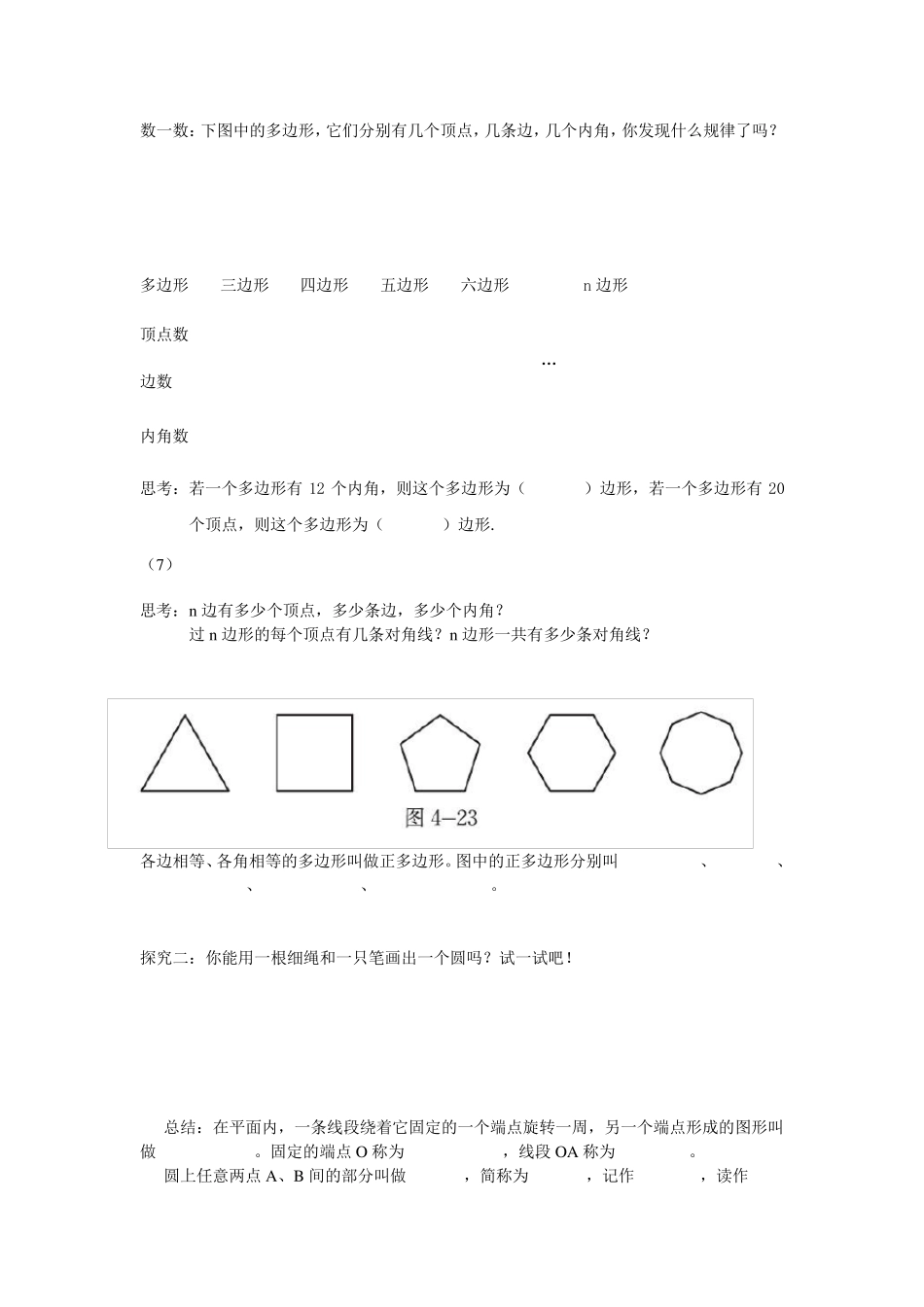
多边形和圆的初步认识 【学习目标】 了解多边形、圆、扇形的相关概念,并能够利用其基本性质解决简单问题 【学习重难点】 学习重点:多边形、圆、扇形的相关概念及相关性质 学习难点:对 n 边形相关特征的探讨。 【学习过程】 一、概念学习 三角形、四边形、五边形、六边形等都是 ,他们都是由 组成的 。 在右图中,多边形ABCDE 的顶点是 ;多边形的边是 多边形的内角(简称多边形的角)有 ; AC、AD 都是连接不相邻两个顶点的线段,像这样的线段叫做多边形的 概念辨析:下面四个图形中,是多边形的是( ) A B C D 探究一: 观察右边四边形ABCD 和五边形ABCDE (1)四边形ABCD 有 个顶点 条边 个内角 过四边形ABCD 的每个顶点有 条对角线 四边形ABCD 总共有 对角线。 (2) 五边形ABCDE 有 顶点 条边 内角 (4) 过五边形ABCDE 的每个顶点有 条对角线 (5) 五边形ABCDE 总共有 对角线。 (6)[ 数一数:下图中的多边形,它们分别有几个顶点,几条边,几个内角,你发现什么规律了吗? 多边形 三边形 四边形 五边形 六边形 … n 边形 顶点数 边数 内角数 思考:若一个多边形有12 个内角,则这个多边形为( )边形,若一个多边形有20个顶点,则这个多边形为( )边形. (7) 思考:n边有多少个顶点,多少条边,多少个内角? 过 n边形的每个顶点有几条对角线?n边形一共有多少条对角线? 各边相等、各角相等的多边形叫做正多边形。图中的正多边形分别叫 、 、 、 、 。 探究二:你能用一根细绳和一只笔画出一个圆吗?试一试吧! 总结:在平面内,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做 。固定的端点O 称为 ,线段 OA 称为 。 圆上任意两点A、B 间的部分叫做 ,简称为 ,记作 ,读作 ;由一条弧AB 和经过这条弧的端点的两条半径O A、O B 所组成的图形叫做 ;顶点在圆心的角叫做 。 补充:圆的面积公式 ;圆的周长公式: 练习:将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,求这三个扇形的圆心角的度数。 变式:将一个圆分成三个大小相同的扇形,那每个扇形的圆心角的度数是 ;若这个圆的半径是2,则其中一个扇形的面积是 。 【随堂练习】 1、若从一个多边形的一个顶点出发,最多可以引10 条对角线,则它是( ) A.十三边形 B.十二边形 C.十一边形 D.十边形 2、观察如图所示图形,回答下列问题:...