并行计算习题及答案例题习题讲解VIP免费

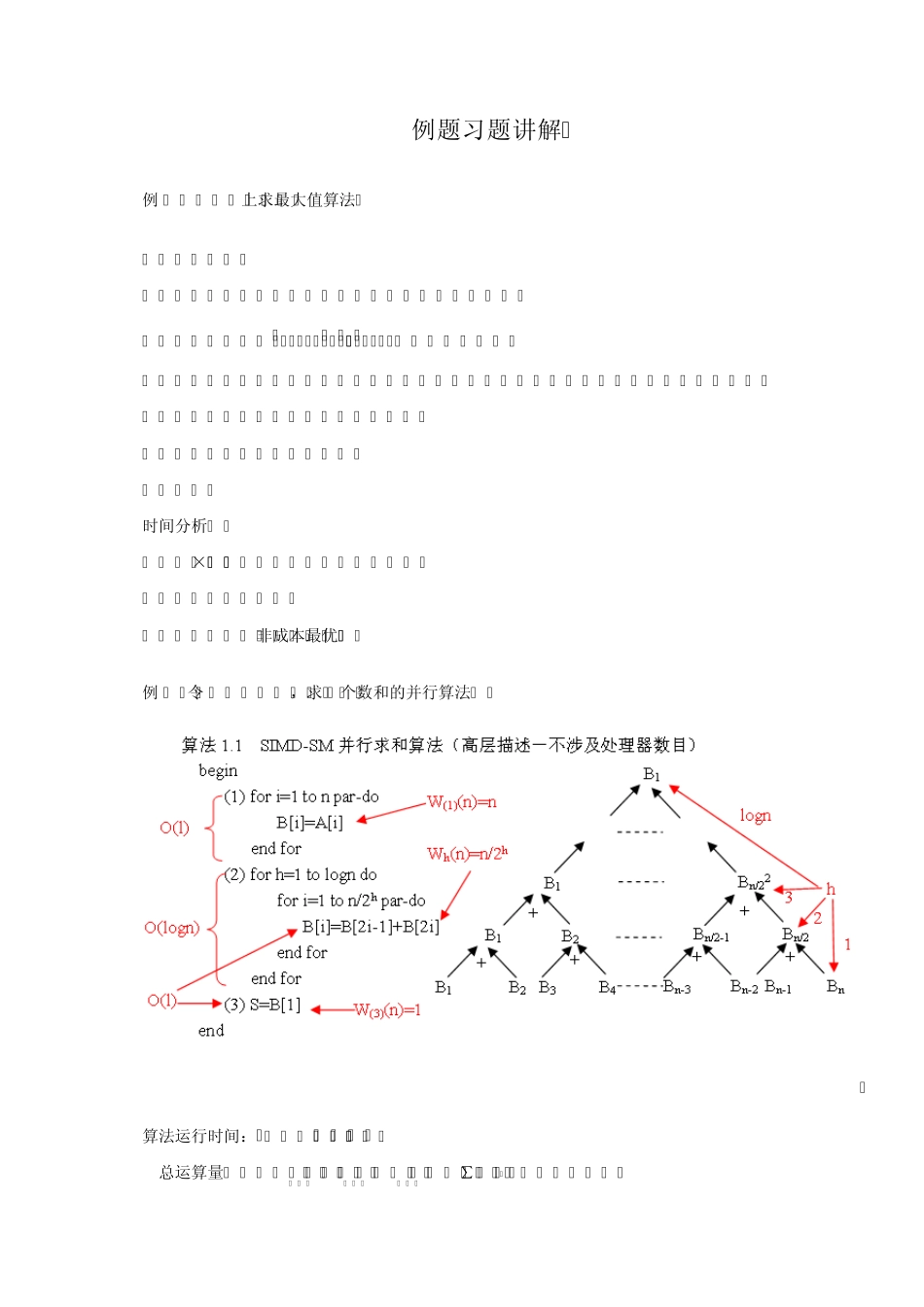
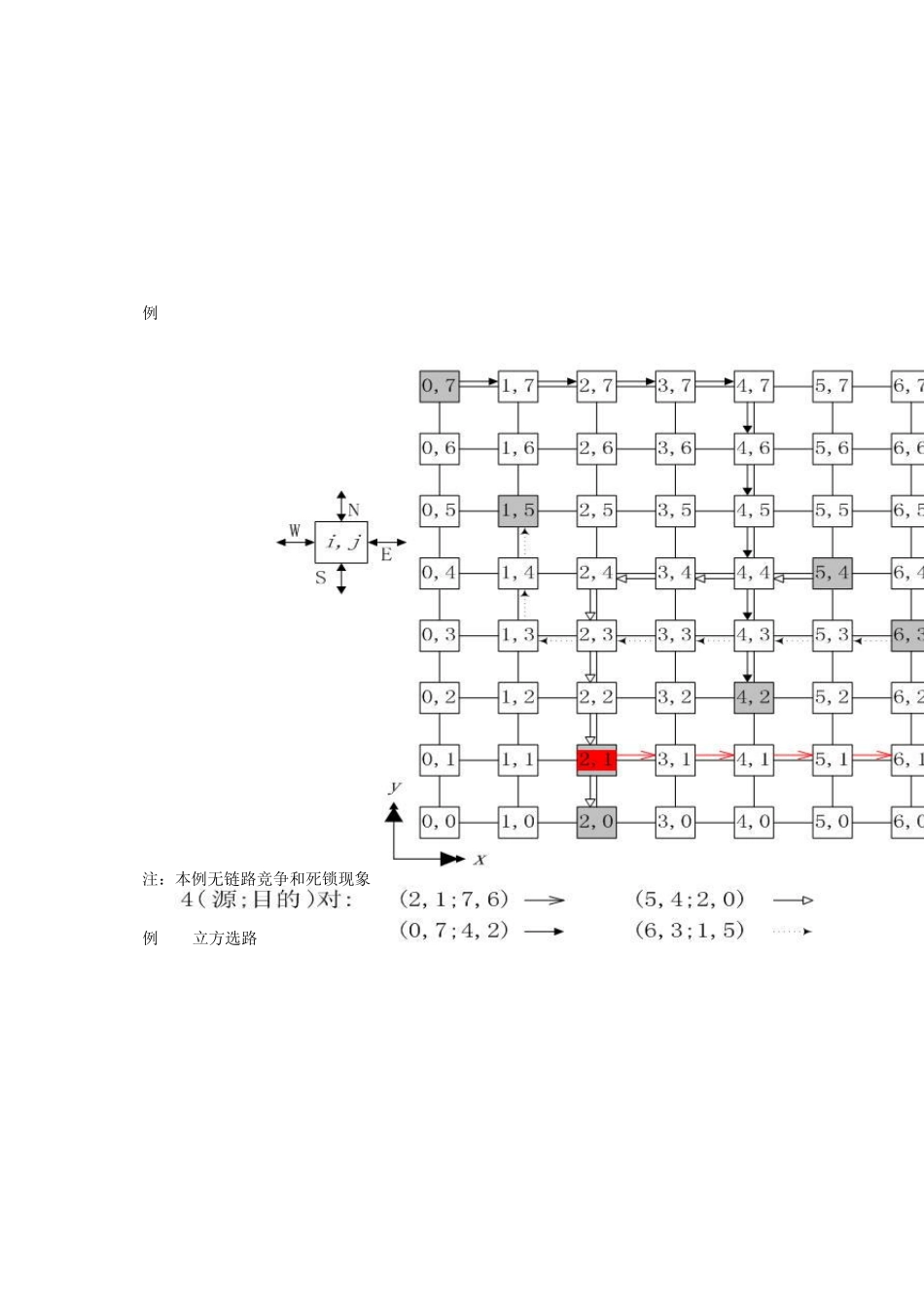
例题习题讲解 例1 SIMD-SM上求最大值算法 Begin for k=m-1 to 0 do for j=2k to 2k+1-1 par-do A[j]=max{A[2j], A[2j+1]} end for end for end 时间分析 t(n)=m×O(1)=O(logn) p(n)=n/2 c(n)=O(nlogn) 非成本最优 例2 令 n=2k(k>=0)，求n个数和的并行算法 算法运行时间：t(n)=O(logn) 总运算量: W(n)=W(1)(n)+W(2)(n)+W(3)(n)=n+∑n/2h+1=O(n) 由Brent定理知: t(n)=O(n/p+logn) 例3 设A为矩阵，有如下串行程序段： for i=1 to n do for j=1 to n do a[3i,2j] = a[3i-2,2j-1] endfor endfor 其相关方向向量为，可知行和列间同时存在数据相关。在此我们可以试用行划分、列划分和方块划分.在行划分的情况下令m=┌n/p┐ ,例1的串行程序段可以转化为如下的并行程序段： for k=1 to P Par-do for i1=1 to m do for j=1 to n do a[3(k-1)m+3i1,2j]=a[ 3(k-1)m+3i1-2 ,2j-1] endfor endfor endfor 例4 设A为一个 n阶方阵，有如下串行程序段： for i=1 to n do for j=1 to n do a[i,j] = a[i-1,j] endfor endfor 分析矩阵A的元素下标 i和j，则 i和j的相关方向向量为，各列之间数据无任何相关关系。因此对矩阵A可按列划分。 串行程序段可转化为如下并行程序段： for k=1 to P Par-do for j1=1 to m do for i=1 to n do a[i,(k-1)m+j1]=a[i-1,(k-1)m+j1] endfor endfor endfor 例5 注：本例无链路竞争和死锁现象 例6 E立方选路 0110(S) 1101(D) 1011(R) 例7 DNS乘法示例 C00=1×(-5)+2×7=9 C01=1×(-6)+2×8=10 C10=3×(-5)+4×7=13 C11=3×(-6)+4×8=14 例 8 上三角方程组的回代解法并行化 (1)SISD上的回代算法 Begin (1)for i=n downto 1 do (1.1)xi=bi/aii (1.2)for j=1 to i-1 do bj=bj-ajixi aji=0 endfor endfor End (2)SIMD-CREW上的并行回代算法 - 划分: p个处理器行循环带状划分 - 算法 Begin for i=n downto 1 do xi=bi/aii for all Pj, where 1≤j≤p do for k=j to i-1 step p do bk=bk-akixi aki=0 endfor endfor endfor End // p(n)=n, t(n)=n 例 9 n=8的BF网络表示 Pr,i与上层Pr-1,i, Pr-1,j相连, 这里j与i仅在第r位不同 例10 一个在MPI中创建新通信域的例子 MPI_Comm MyWorld, SplitWorld; int my_rank,group_size, Color...