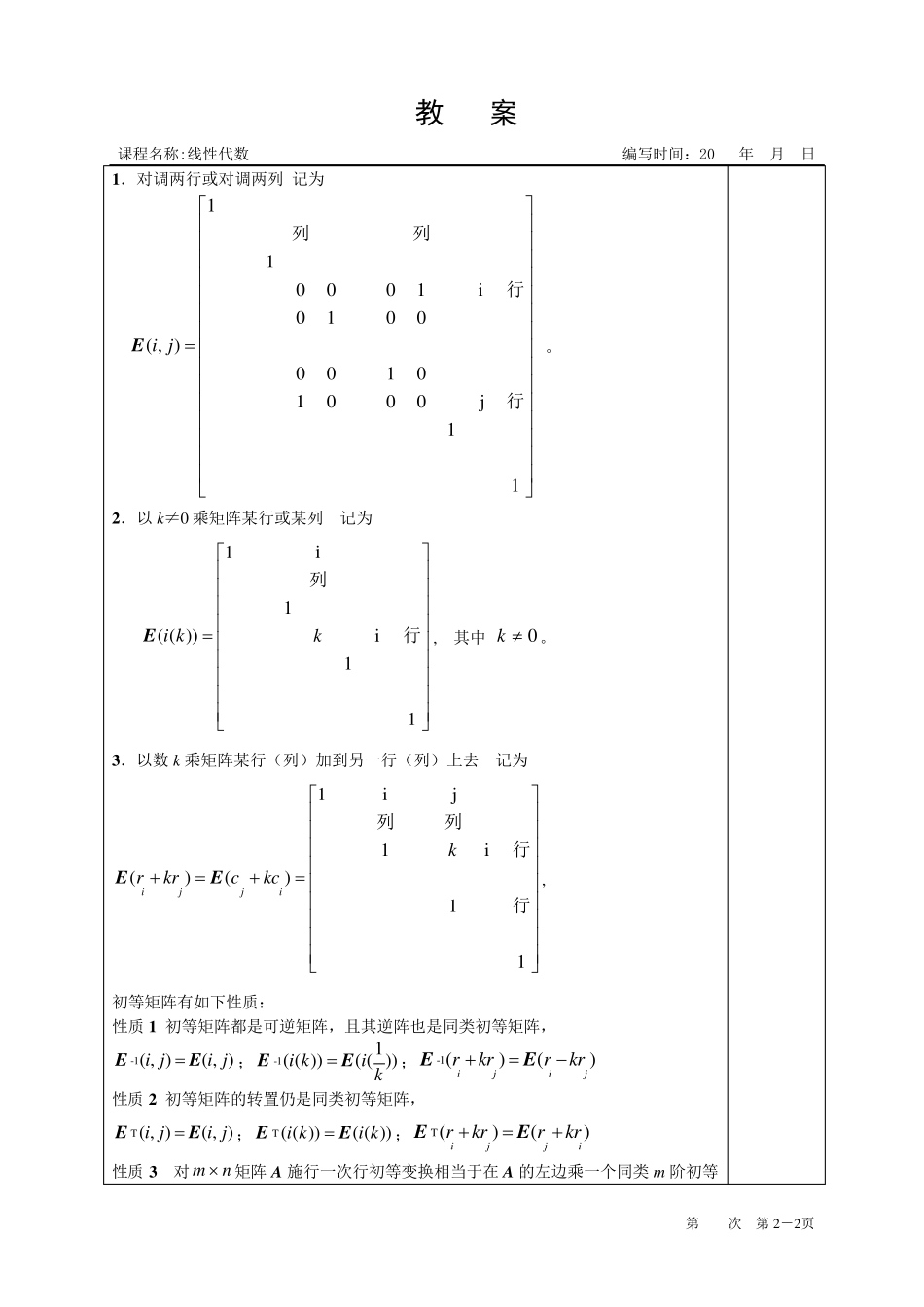
教 案 课程名称:线性代数 编写时间:20 年 月 日 第 次 第2-1页 授课章节 第三章 矩阵的初等变换与线性方程组 §1 矩阵的初等变换 §2 初等矩阵 目的要求 理解初等变换、初等矩阵,掌握逆阵求法 重点难点 利用初等变换法求逆阵 复习……………………………………………………………………………………3 分钟 §1 矩阵的初等变换 定义 1 下面三种变换称为矩阵的初等行(列)变换: (1)互换矩阵中两行(列)元素(记 ri←→rj 或 ci←→c j ); (2)用一个非零数k 乘矩阵的某一行(列)(记 k×ri 或 k×ci ); (3)矩阵的某一行(列)元素k 倍地加到另一行(列)对应元素上(记 ri +k×rj 或 ci + k×c j );(注意:本行的元素并没有改变) 矩阵的初等行或列变换统称矩阵的初等变换。 如果矩阵A 经过有限次的初等变换变成 B ,则称A 与B 等价。记做 A ~ B 或 A →B 。矩阵等价的三个性质: (1)反身性 A →A ; (2)对称性 若 A →B ,则 B →A ; (3)传递性:若 A →B ,B →C ,则 A →C 。 行阶梯形矩阵:可画出一条阶梯线,线的下方全为零,每个台阶只有一行,即每段竖线的长度为一行,竖线后面的第一个元素为非零数。如 210101200000,210100210000,010100200003 等都是行阶梯形矩阵。 行最简形矩阵:在行阶梯形矩阵的基础上,每个非零行左数第一个非零元是1,并且它所在列的其它元素都是零。 标准型矩阵:它的左上角为一个单位阵,其它元素都是零。就是000rm nE. 定理 1 任意一个 m×n 矩阵A ,总可以经过有限次初等行变换将其变成行阶梯形矩阵,进一步还可化成行最简形矩阵。 定理 2 一个非奇异 矩阵A ,可以经过有限次初等行变换变成单位阵。 定理 3 任意一个 m×n 矩阵A ,总可以经过有限次初等变换将其变成标准型矩阵。 例 1 用初等行变换将021382130A化成单位阵。 …………………………………………………………………………………………42 分钟 §2 初等矩阵 定义 2(初等矩阵)对单位矩阵E 施 行一次初等变换后得 到的矩阵,称为初等矩阵。有以下三种类 型:对调 、倍乘、倍加, 教 案 课程名称:线性代数 编写时间:20 年 月 日 第 次 第2-2页 1 .对调两行或对调两列...