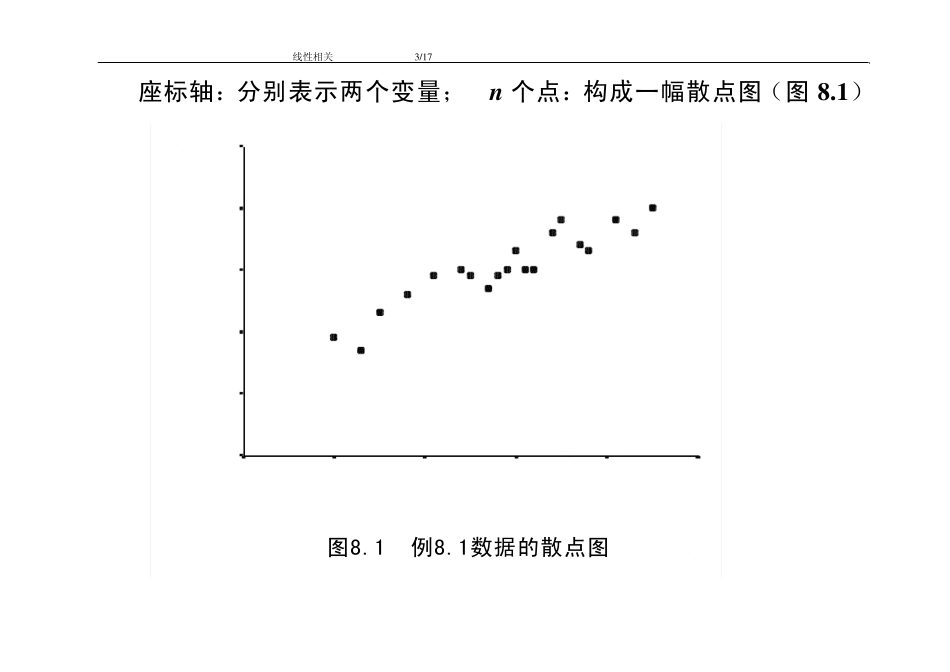
第八章 线 性 相 关 前面着重于描述某一变量的统计特征 或比较该变量的组间差别 两个随机变量之间的关系: 如体重与肺活量、 年龄与血压 是否存在线性联系?正向还是负向?联系的程度? 线性相关(linear correlation):线性联系?方向?程度? 8.1 线 性 相 关 概 念 1. 独立随机的双变量正态分布样本 讨论两个变量X 和 Y 的相关性。 样本:独立的、成对的观察值 (x 1,y 1),(x 2,y 2),„,(x n,y n) 第八章 线性相关 2 例8.1 为讨论父子身高间的线性相关程度,南方某地在应届中学毕业生花名册中随机抽取20 名男生,分别测量他们和他们的父亲的身高(cm),得样本资料如表8.1 所示。 表8.1 20 对父子的身高(cm)数据 编号 1 2 3 4 5 6 7 8 9 10 父高X 150 153 155 158 161 164 165 167 168 169 子高Y 159 157 163 166 169 170 169 167 169 170 编号 11 12 13 14 15 16 17 18 19 20 父高X 170 171 172 174 175 177 178 181 183 185 子高Y 173 170 170 176 178 174 173 178 176 180 问如何保证这是一份可供讨论线性相关的合格样本? 解 (1)随机抽取; (2)互相独立? 2. 散点图 (scatter plot) 线性相关 3 /1 7 座标轴:分别表示两个变量; n 个点:构成一幅散点图(图 8 .1 ) 图8.1 例8.1数据的散点图X190180170160150140Y190180170160150140 第八章 线性相关 4 图8 .2 典型散点图 线性相关 5/17 图(a)和(c),正相关(positive correlation) 图(b)和(d),负相关(negative correlation) 图(e) 、(f) 、(g),Y 和X 无关联 图 (h),可能存在曲线型联系。 通常所说的相关就是线性相关,(e)到(h)均属不相关 对于不相关的情形,宜进一步澄清是否为曲线关系 8.2 相 关 系 数 Pearson 积矩相关系数(product-moment correlation coefficient) 对双变量正态分布变量 X 和Y 的 方 差 )的方差(的协方差和相关系数)(YYXX (8.1) 第八章 线性相关 6 总体相关系数,记为 =0,X 和Y 无线性相关或零相关(nu ll correlaton) >0, 正相关 <0, 负相关 =1 或-1, 完全相关(罕见!)。 样本相关系数,记为r 对于 n 对随机样本,X 和Y 的样本协方差: 11))((1nlnyyxxYXxyniii的样本协方差和 (8.2) lxy:X 与 Y 的离均差乘...