球的接切问题VIP免费

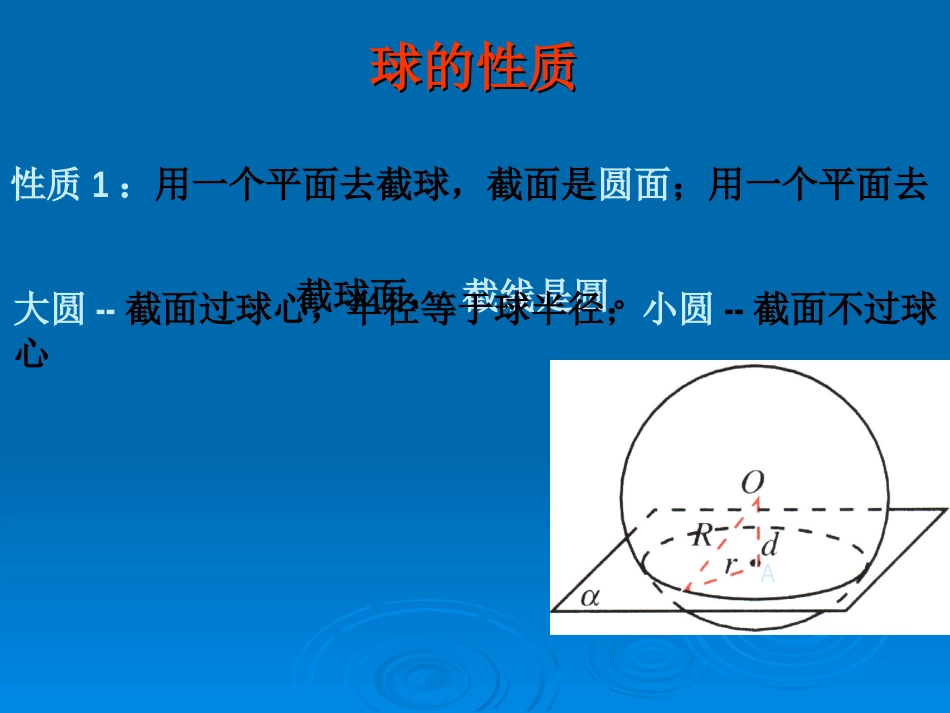
<<<<多面体外接球的半径的求法多面体外接球的半径的求法>>>>球的性质球的性质性质1：用一个平面去截球，截面是圆面；用一个平面去截球面，截线是圆。大圆--截面过球心，半径等于球半径；小圆--截面不过球心A球与正方体的“切”“接”问题aR2位置关系描述：球与正方体的六个面都相切，各个面的中心即为切点。正方体的中心即为球心。相对两个面中心连线即为球的直径。球叫做“正方体的内切球”，正方体叫做“球的外切正方体”。o图形度量关系球的直径等于正方体棱长。一、正方体的内切球aR22位置关系描述：度量关系图形二、球与正方体的棱相切球与正方体的12条棱都相切，各棱的中点即为切点。正方体中心即为球心。“对棱”中点连线即为球的直径。球的直径等于正方体一个面上的对角线长图形位置关系描述：度量关系三、正方体的外接球正方体的8个顶点在同一个球面上。正方体的中心即为球心。球叫做“正方体的外接球”，正方体叫做“球的内接正方体”。正方体的（体）对角线等于球直径aaaaR32222例1已知一个正方体内接于一个球，若过球心作一截面，则所得截面可能是()A．①②B．②④C．①②③D．②③④答案：C[解析]当截面不平行于任一侧面，也不过体对角线时，所得截面为①；当截面过正方体体对角线时，所得截面为②；当截面平行于正方体的一个侧面时，所得截面为③；但是无论如何截面都不会为④.正方体外接球第二种截面第三种截面多面体外接球的半径的求法方法一：直接法方法二：构造直角三角形方法三：补形一、直接法OAO1BA1AC1CO2010年文(7)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为（A）3a2（B）6a2（C）12a2（D）24a2B直接法的使用技巧2222abclabcR设长方体的长、宽、高分别为、、，则,23aRa设正方体的边长为则有变式1：已知长方体1111DCBAABCD的长宽高分别为3,4,5,则该长方体的外接球的表面积等于_________。2010年理设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为二、构造直角三角形2211OBOOOB构造直角三角形使用技巧ROCB22,r,2llRr设柱体的高为底面外接圆的半径为则有任意直棱柱的外接球圆柱的外接球如何求直棱柱的外接球半径呢？（1）先找外接球的球心：它的球心是连接上下两个多边形的外心的线段的中点；（2）再构造直角三角形，勾股定理求解。构造直角三角形使用技巧AOO1AOO1圆锥的外接球22,r,hRrhR设椎体的高为底面外接圆的半径为则有正棱椎的外接球例：已知正四棱锥的底面边长为a,侧棱长为a2，求它的外接球的半径：解析：连接AC与BD交于E,在正四棱锥S-ABCD中，所以SE是棱锥的高，设球心为O，球的半径为R,知球心O在高AE上，在直角三角形OEC中，222OEECOC2222222a,262622263ACECaSESCECaaRaRRa构造直角三角形使用技巧球心在几何体外部222)(hRrRrh则有，，底面外接圆的半径为设椎体的高为球心在几何体内部222)(RhrRrh则有，，底面外接圆的半径为设椎体的高为226.4Ra将正四面体放到正方体中，得正方体的棱长为a,且正四面体的外接球即正方体的外接球，所以＝-aPABC例4：求棱长为的正四面体的外接球的表面积。三、补形法222222222123322bbcabcR将正四面体放到长方体中，边长为a,b,c,则有：acaABCDAB=CD=2AC=BD=3AD=BC=1变式：四面体，，，，求其外接球体积三、补形法对棱相等的四面体三、补形法5P-ABCABCPA=8PB=PC=73AB=3例：已知三棱锥中，三角形为等边三角形，且，，，则其外接球的体积为补形法的使用技巧根据题中给出的线面位置关系，将其放到特殊的几何体中，转化为直接法或构造直角三角形法。构造直角三角形使用技巧AOO1AOO1椎体的外接球22,r,hRrhR设椎体的高为底面外接圆的半径为则有补形法的使用技巧根据题中给出的线面位置关系，将其放到特殊的几何体中，转化为直接法或构造直角三角形法。特例1出现两个垂直关系，利用直角三角形结论。【原理】：直角三角形斜边中线等于斜边一半。球心为直角三角形斜边中点。OABCPAC是球的直径