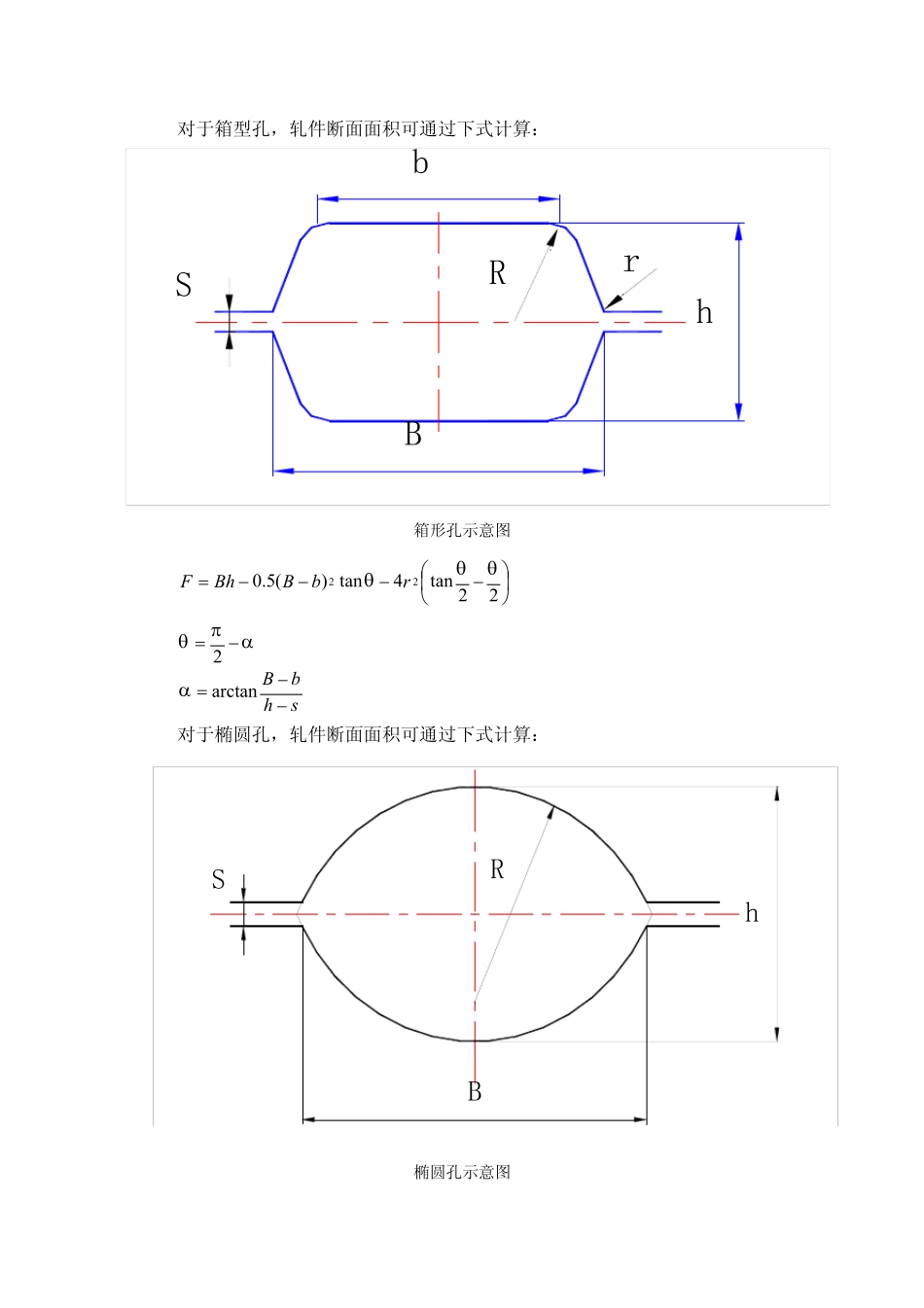
1 轧制过程数学模型 1.1 轧制工艺参数模型 随着科学技术的发展,计算机已广泛应用于轧钢生产过程的控制,促使轧钢生产向自动化、高速和优质方向发展。电子计算机在线控制生产过程,不仅仅只是电子计算机本身的硬件和软件的作用,更重要的是控制系统和各种各样的数学模型,正因为有适合轧钢生产的各种数学模型,才有可能实现电子计算机对整个轧钢生产各个环节的控制,获得高精度的产品。 线材连轧生产过程的主要内容基本上可归纳为尺寸变化和温度变化两大类性质极不相同但又相互紧密联系的物理过程,涉及的数学模型主要是轧制工艺参数的制定、各环节的温降变化、产品质量控制及实现线材连轧生产的可靠性等。 在线材连轧生产过程中,准确地计算(预估)各个环节的温度变化是实现计算机控制的重要前提,这是因为轧件各道次的变形阻力、轧制压力、轧制力矩的准确确定与温度是分不开的,而各机架轧制压力的预估精度将直接关系到设备的使用安全等。 下面分别讨论线材连轧生产过程中的温降模型、变形阻力模型、轧制力与轧制力矩模型。 1.1.1 延伸系数及孔型尺寸计算模型 在制订棒线材轧制工艺时,当坯料和产品断面面积F0和Fn给定之后,总延伸系数Σµ 就可唯一确定: nnniiniFFFFFFFFFF011211021===−+ΣΛΛΛΛµµµµµ 其中:n——总轧制道次; µi——某一道次的延伸系数; Fi——某一道次的轧件断面面积。 对于箱型孔,轧件断面面积可通过下式计算: 箱形孔示意图 ⎟⎠⎞⎜⎝⎛−−−−=22tan4tan)(5.022θθθrbBBhF απθ−= 2 shbB−−= arctanα 对于椭圆孔,轧件断面面积可通过下式计算: SBbhRrShBR 椭圆孔示意图 m BRF+−=)sin(2θθ RB2arcsin2=θ ⎟⎠⎞⎜⎝⎛ −−=2cos12θRhm 对于圆孔,轧件断面面积可通过下式计算: R30°30°SD1B30°30°圆孔示意图 απθ2−= αθtan422RRF+= 1.1.2 前滑模型 孔型轧制时的前滑率计算可采用筱篬或斋藤提出的实验模型。两者都认为前滑仅是轧件、孔型几何尺寸的函数。斋藤模型以平均工作辊径定义前滑,当道次变形量较小时会出现负前滑的计算结果;筱篬模型改用孔型槽底处的最小辊径定义前滑,即前滑Sf为: Sf=V1/VR-1 (1.1) 其中: V1 ,VR——轧件出口速度及孔型槽底处的轧辊线速度。 在孔型中轧制时,前滑值取平均值fS ,其计算式为 ()[]1cos1cos++−=hhDS fγγ ⎟⎟⎠⎞⎜⎜⎝⎛ +=βααγ212 DhH −−= 1cosα 式中 γ ——变形区中...