运筹学第四章VIP免费

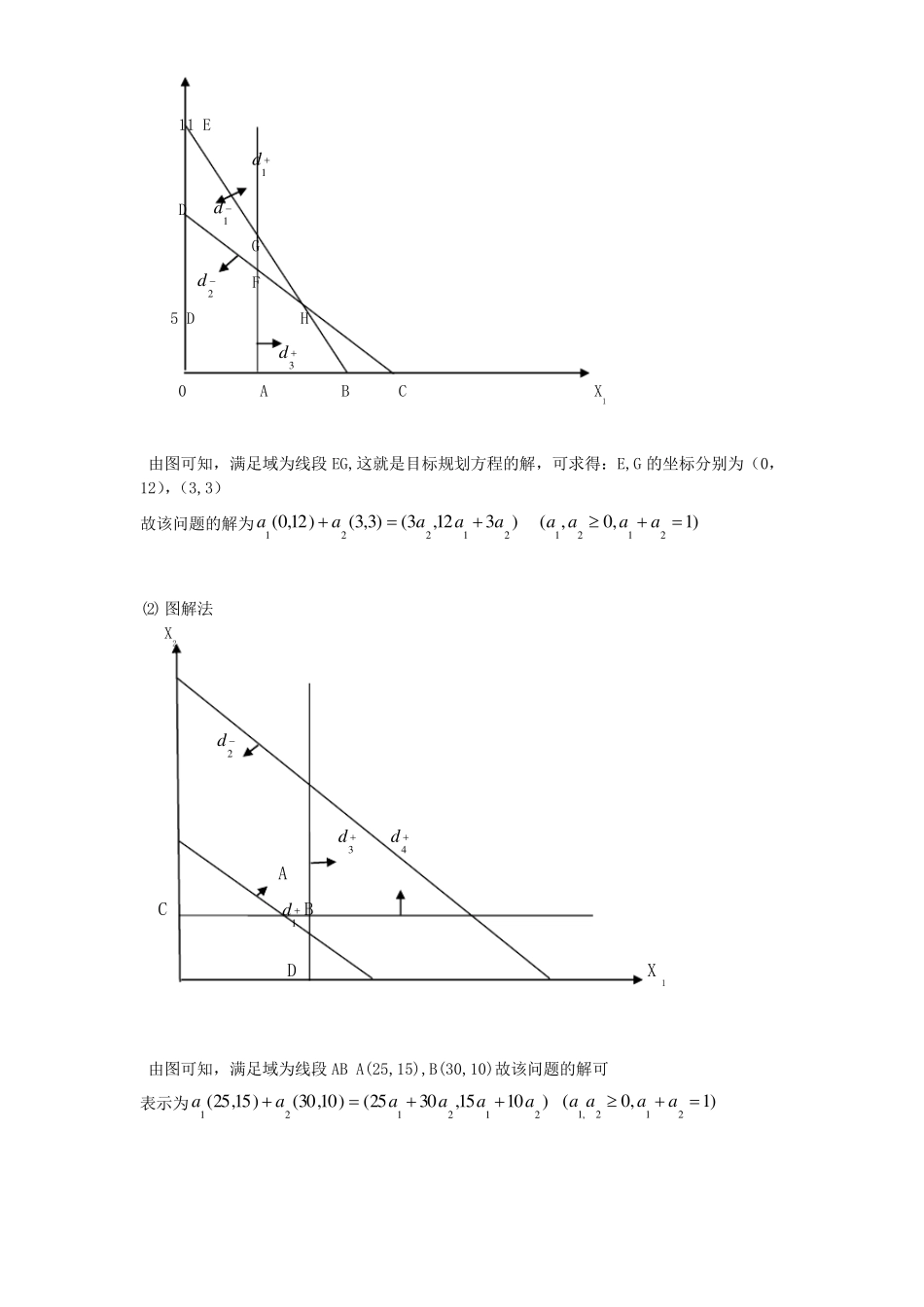
运筹学第四章习题答案 4.1 若用以下表达式作为目标规划的目标函数，其逻辑是否正确？为什么？ （1）max｛d -d ｝ （2）max｛d +d ｝ （3）min｛d +d ｝ （4）min｛d -d ｝ （1）合理，令f（x）+d -d =b,当f（x）取最小值时，d -d 取最大值合理。 (2)不合理，d 取最大值时，f（x）取最大值，d 取最大值时，f（x）应取最小值 （3）合理，恰好达到目标值时，d 和d 都要尽可能的小。 （4）合理，令f（x）+d -d =b,当f（x）取最大值时，d -d 取最小值合理。 4.2 用图解法和单纯形法解下列目标规划问题 （1）min｛P13d ，P22d ，P3 （1d +1d ）｝ 24261121ddxx 52221ddxx 155331ddx 3,2,1,0,,,21iddxxii （2）min{P1( 43dd),P21d ,P32d ,P4 ( 435.1 dd)} 401121ddxx 1002221ddxx 30331ddx 15442ddx 4,3,2,1,0,,,21iddxxii (1)图解法 11 E 1d D 1d G 2d F 5 D H 3d 0 A B C X1 由图可知，满足域为线段 EG,这就是目标规划方程的解，可求得：E,G 的坐标分别为（0，12），（3,3） 故该问题的解为)31 2,3()3,3()1 2,0(21221aaaaa )1,0,(2121aaaa (2) 图解法 X2 2d 3d 4d A C 1d B D X1 由图可知，满足域为线段 AB A(25,15),B(30,10)故该问题的解可 表示为)1 01 5,3 02 5()1 0,3 0()1 5,2 5(212121aaaaaa )1,0(212,1aaaa (1)单纯形法 0 0 P1 0 0 P2 P3 P3 CB XB x1 x2 b P3 P2 0 6 2 0 0 0 0 -1 1 24 5 15 2 1 0 0 -1 1 0 0 5 0 -1 1 0 0 0 0 P1 P2 P3 0 0 1 0 0 0 0 0 -1 -1 0 0 1 0 0 0 -6 -2 0 0 0 0 2 0 P3 P2 0 x1 0 2 1.2 -1.2 0 0 -1 1 6 2 3 0 1 0.2 0.2 -1 1 0 0 1 0 -0.2 0.2 0 0 0 0 P1 P2 P3 0 0 1 0 0 0 0 0 0 -1 -0.2 0.2 1 0 0 0 0 -2 -1.2 1.2 0 0 2 0 P3 0 0 x2 x1 0 0 0.8 -0.8 2 -2 -1 1 2 2 3 0 1 0.2 -0.2 -1 1 0 0 1 0 -0.2 0.2 0 0 0 0 P1 P2 P3 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 -0.8 0.8 -2 2 2 0 0...