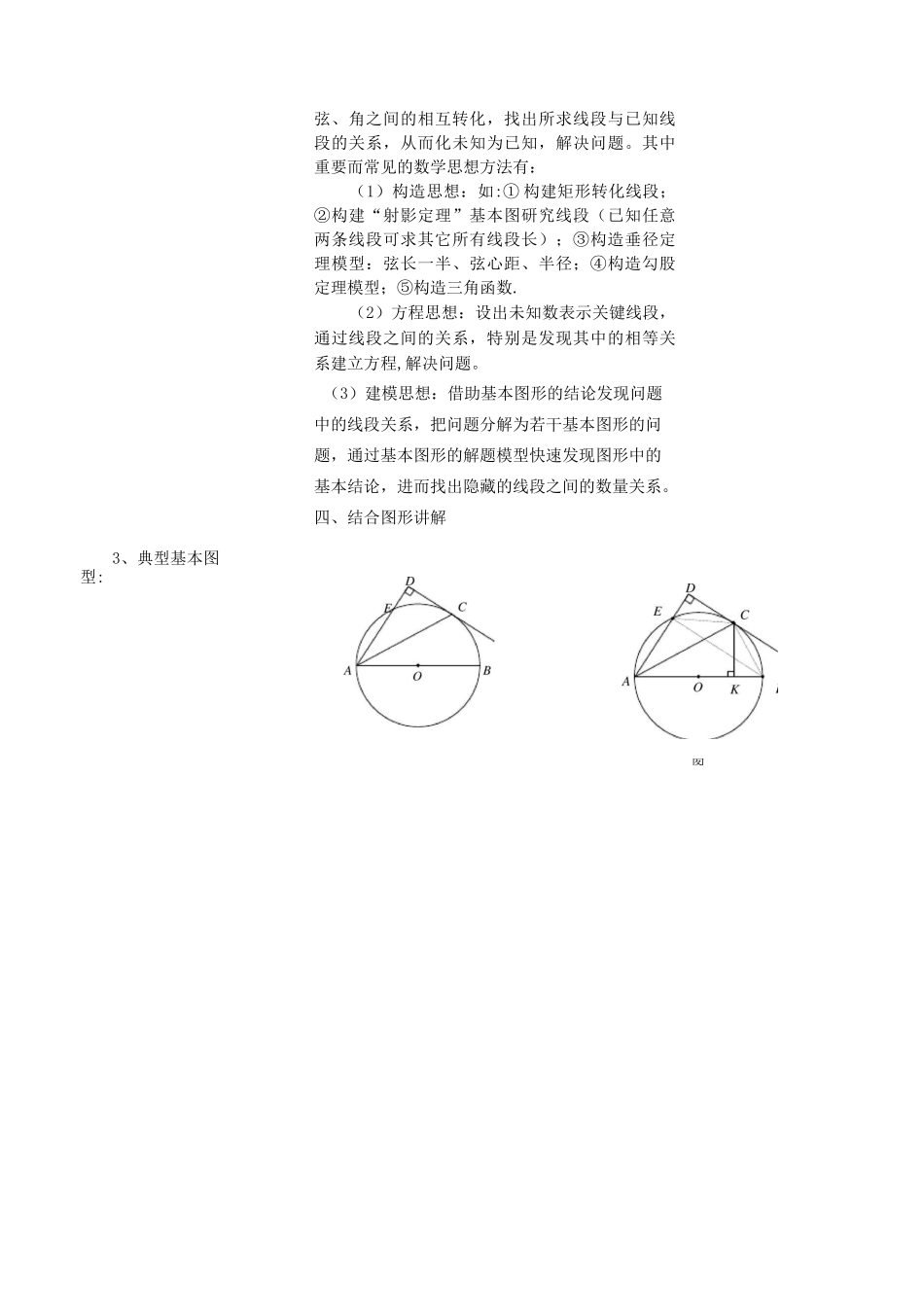
圆的证明与计算综合复习提升圆的证明与计算综合复习提升教学内容考题形式分析:主要以解答题的形式出现,第 1 问主要是判定切线;第 2 问主要是与圆有关的计算:①求线段长(或面积);② 求线段比;③求角度的三角函数值(实质还是求线段比)。解题秘笈:1、判定切线的方法:(1)若切点明确,则“连半径,证垂直”常见手法有:全等转化;平行转化;直径转化;中线转化等;有时可通过计算结合相似、勾股定理证垂直;(2)若切点不明确,则“作垂直,证半径”常见手法:角平分线定理;等腰三角形三线合一,隐藏角平分线;总而言之,要完成两个层次的证明:①直线所垂直的是圆的半径(过圆上一点);②直线与半径的关系是互相垂直。在证明中的关键是要处理好弧、弦、角之间的相互转化,要善于进行由此及彼的联想、要总结常添加的辅助线.2、与圆有关的计算:计算圆中的线段长或线段比,通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合,形式复杂,无规律性。分析时要重点注意观察已知线段间的关系,选择定理进行线段或者角度的转化。特别是要借助圆的相关定理进行弧、授课日期3、典型基本图型:图弦、角之间的相互转化,找出所求线段与已知线段的关系,从而化未知为已知,解决问题。其中重要而常见的数学思想方法有:(1)构造思想:如:① 构建矩形转化线段;②构建“射影定理”基本图研究线段(已知任意两条线段可求其它所有线段长);③构造垂径定理模型:弦长一半、弦心距、半径;④构造勾股定理模型;⑤构造三角函数.(2)方程思想:设出未知数表示关键线段,通过线段之间的关系,特别是发现其中的相等关系建立方程,解决问题。(3)建模思想:借助基本图形的结论发现问题中的线段关系,把问题分解为若干基本图形的问题,通过基本图形的解题模型快速发现图形中的基本结论,进而找出隐藏的线段之间的数量关系。四、结合图形讲解如图 1:AB 是 0O 的直径,点 E、C 是 0O 上的两点,基本结论有:(1) 在“AC 平分 ZBAE”;“AD 丄 CD”;“DC是 0O 的切线”三个论断中,知二推(2) 如图(4):若 CK 丄 AB 于 K,贝 9:-1① CK=CD;BK=DE;CK=-BE=DC;2<② /ADCsAACB=AC2=AD・AB例题讲解如图 1:AB 是 0O 的直径,点 E、C 是 0O 上的两点,在“AC 平分 ZBAE”;“AD 丄 CD”(1) 求证:DC 是 0O 的切线(2) 若 CKLAB 于 K① 小明通过探究发现 CK=2BE,你认为是否正确,请说明原因。② 请证明...