应力和应变间的关系VIP免费

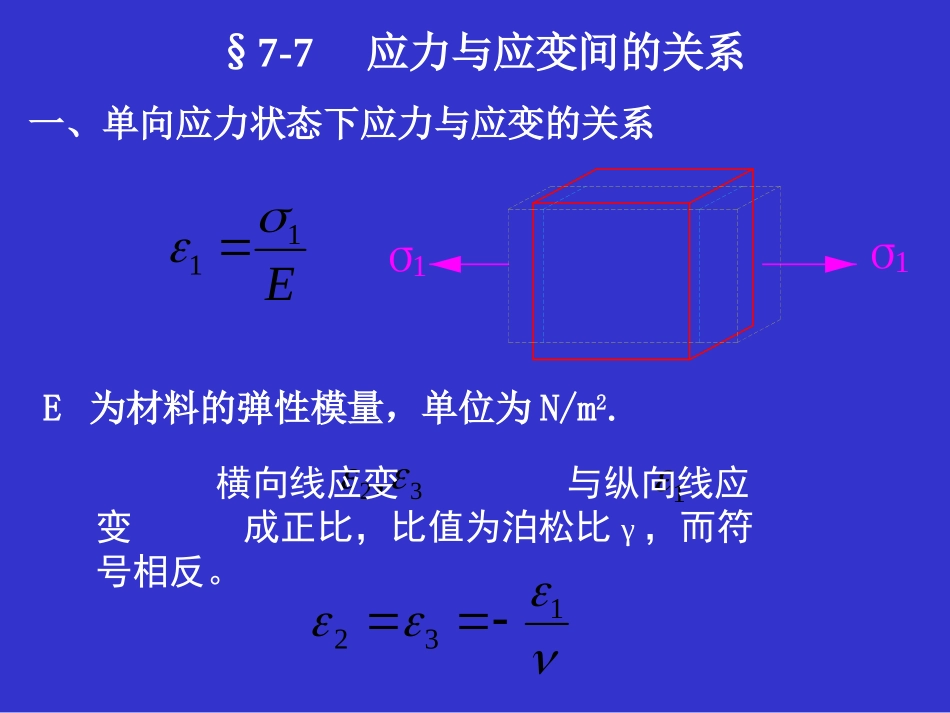
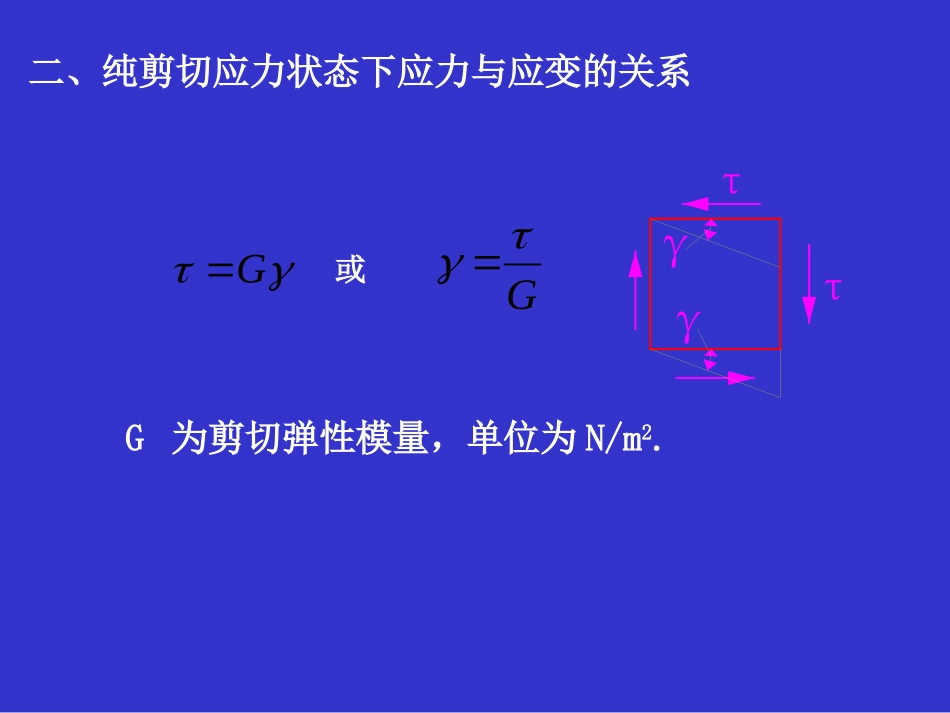
§7-7应力与应变间的关系一、单向应力状态下应力与应变的关系32,E111横向线应变与纵向线应变成正比，比值为泊松比γ，而符号相反。132σ1σ1E为材料的弹性模量，单位为N/m2.二、纯剪切应力状态下应力与应变的关系ττγγGG或G为剪切弹性模量，单位为N/m2.（1）符号规定xyzo上面右侧面前面σxτxyτxzσyτyxτyzσzτzxτzyxyzxyyzzxxyzxyyzzx1、各向同性材料的广义胡克定律(a)(a)三个正应力分量三个正应力分量：拉应力为正压应力为负。三、复杂应力状态下应力与应变的关系τxyτxzσxxyzo上面右侧面前面σyτyxτyzσzτzxτzy(b)(b)三个剪应力分量三个剪应力分量::若正面(外法线与坐标轴正向一致的平面)上剪应力矢的指向与坐标轴正向一致,或负面(外法线与坐标轴负向一致的平面)上剪应力矢的指向与坐标轴负向一致，则该剪应力为正,反之为负。图中表示的均为正方向图中表示的均为正方向线应变线应变:以伸长为正,缩短为负。剪应变剪应变:使直角减小者为正,增大者为负。γxyγyzγzxxOyyOzzox。σxxyzO上面右侧面前面σyτyxτyzσzτzxτzyτxyτxz在xyz分别单独存在时,x方向的线应变x依次为:Exx'2、各向同性材料的广义胡克定律Eyx"Ezx'"σyσyσxσxxxzσzσz(1)线应变的推导在xyz同时存在时,x方向的线应变x为)(1zyxxE)]([1)]([1yxzzxzyyEE在xyz同时存在时,y,z方向的线应变为剪应变xy,yz,zx与剪应力xy,yz,zx之间的关系为GGGzxzxyzyzxyxy公式的适用范围公式的适用范围::在线弹性范围内,小变形条件下,各向同性材料。(2)剪应变的推导)]([1)]([1)(1yxzzxzyyzyxxEEEGGGzxzxyzyzxyxy公式的适用范围公式的适用范围::在线弹性范围内,小变形条件下,各向同性材料。3、特例（1）平面应力状态下(假设Z=0))(1yxxE)(1xyyE)(yxzEGxyxy（2）广义胡克定律用主应力和主应变表示时三向应力状态下：)]([13211E)]([11322E)]([12133E(7-7-6)平面应力状态下设3=0,则)(1211E)(1122E)(213E材料的三个弹性常数材料的三个弹性常数E,G,E,G,间存在如下关系间存在如下关系::)1(2vEG例题7-6已知一受力构件自由表面上的两主应变数值为10160,102406361。构件材料为Q235钢，其弹性模量E=210GPa，泊松比=0。3。求该点处的主应力值，并求该点处另一主应变2的数值和方向。ε1ε3ε213σ2σσ=0物体表面解：32321,,,,1与一，一对应。由于构件自由表面，所以主应力2=0。所以该点为平面应力状态。)(1311E)(1133EMPaE3.44)(13121MPaE3.20)(11323由解得该点处另一主应变2的数值为103.34)(6312E2是缩短的主应变，其方向必与1和3垂直，即沿构件的外法线方向。四、各向同性材料的体积应变（2）各向同性材料在空间应力状态下的体积应变（1）概念:构件每单位体积的体积变化,称为体积应变用θθ表示。)1()1()1('321dzdydxV公式推导设单元体的三对平面为主平面,其三个边长为dx,dy,dz变形后的边长分别为dx(1+,dy(1+2,dz(1+3,因此变形后单元体的体积为:213dxdydz体积应变为体积应变为321321321)1()1()1()1('dxdydzdxdydzdxdydzdxdydzdxdydzdzdydxVVV)(21321E将广义胡克定律)]([13211E)]([11322E)]([12133E代入得321)(21zyxE在最一般的空间应力状态下，材料的体积应变只与三个线应变x，y，z有关。仿照上述推导有在任意形式的应力状态下,各向同性材...