指数体系和因素分析VIP免费

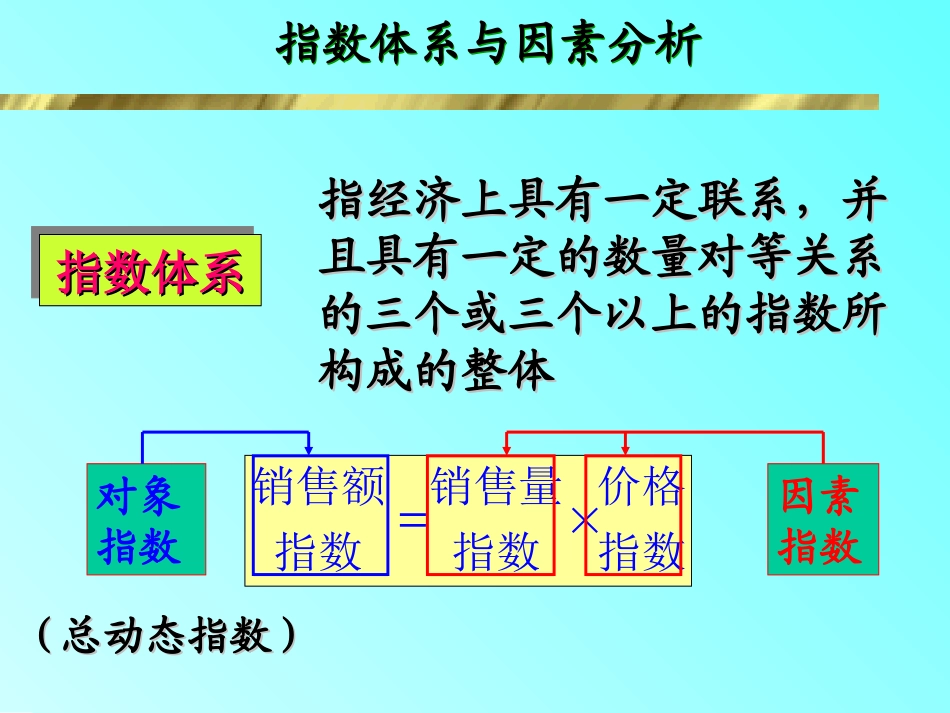
指数体系指数体系指数体系指数体系指经济上具有一定联系，并指经济上具有一定联系，并且具有一定的数量对等关系且具有一定的数量对等关系的三个或三个以上的指数所的三个或三个以上的指数所构成的整体构成的整体指数价格指数销售量指数销售额因素指数对象指数（总动态指数）（总动态指数）指数体系与因素分析指数体系与因素分析⑴⑴相对数形式相对数形式：：————对象指数等于各个对象指数等于各个因素指数的连乘积因素指数的连乘积⑵⑵绝对数形式：绝对数形式：————对象指数的增减对象指数的增减额额等于各因素指数影响的增减额之和等于各因素指数影响的增减额之和)()(011100010011PQPQPQPQPQPQPQPQKPQPQKPQPQkPQPQ011100010011指数体系的基本形式指数体系的基本形式指数体系的基本形式指数体系的基本形式指数体系的作用指数体系的作用指数体系的作用指数体系的作用⒈利用指数体系可进行指数之间的相互推算；⒉对单个指数的编制具有指导意义；⒊利用指数体系可进行因素分析。利用指数体系对现象的综合变动利用指数体系对现象的综合变动从数量上分析其受各因素影响的从数量上分析其受各因素影响的方向、程度及绝对数额方向、程度及绝对数额指标符号2012年2013年工资总额(万元)职工人数（人）平均工资(元/人)EEffXX5001000500056710505400【【例例】】已知某企业工资的资料如下，计算已知某企业工资的资料如下，计算工资总额的变动并对其进行因素分析。工资总额的变动并对其进行因素分析。简单现象总体总量指标变动的两因素分析简单现象总体总量指标变动的两因素分析简单现象总体总量指标变动的两因素分析简单现象总体总量指标变动的两因素分析【【分析分析】】011010101100100101011011001001XXfffXfXfXfXfXEEXXfffXfXfXfXEEXfE平均工资职工人数工资总额简单现象总体因素分析的特点：简单现象总体因素分析的特点：相对数分析可以不引入同度量因素，但绝对数分析必须引入同度量因素【【解解】】万元万元万元﹪﹪﹪综合影响：万元﹪为：受平均工资变动的影响万元﹪为：受职工人数变动的影响其中：万元﹪；工资总额的变动：4225671081054.11334250005400105010850005400225100010505000105100010501675005674.11350056701101010010101XXfXXkffXffkEEEEkXfE商品名称计量单位销售量价格（元）销售额（元）基期报告期基期报告期甲件1201002025240025002000乙支1000120045400060004800丙台60100290300174003000029000合计—————2380038500358000Q1P0P1Q00PQ11PQ01PQ【【例例】】计算销售总额的变动并对其进行因素分析计算销售总额的变动并对其进行因素分析复杂现象总体总量指标变动的两因素分析复杂现象总体总量指标变动的两因素分析复杂现象总体总量指标变动的两因素分析复杂现象总体总量指标变动的两因素分析【【解解】】元元元﹪﹪﹪综合影响：元﹪受价格变动的影响为：元﹪：受销售量变动的影响为其中：元﹪销售总额的变动：2700120001470054.10742.15076.16132700358003850054.1073580038500212000238003580042.1502380035800114700238003850076.1612380038500011101110001000100110011PQPQPQPQKPQPQPQPQKPQPQPQPQkPQPQffXfXfX各组水平各组结构即：即：总体平均水平同时受各组水总体平均水平同时受各组水平和各组结构两个因素的影响平和各组结构两个因素的影响平均指标变动的两因素分析平均指标变动的两因素分析平均指标变动的两因素分析平均指标变动的两因素分析构造指数体系如下构造指数体系如下：：11011100011000011101ffXffXffXffXffXffXXX相对数形式：=×可变构成指数结构变动影响指数固定构成指数记为nXnnXXXXXXffXffXffXffXffXffX...