坐标系极坐标系VIP免费

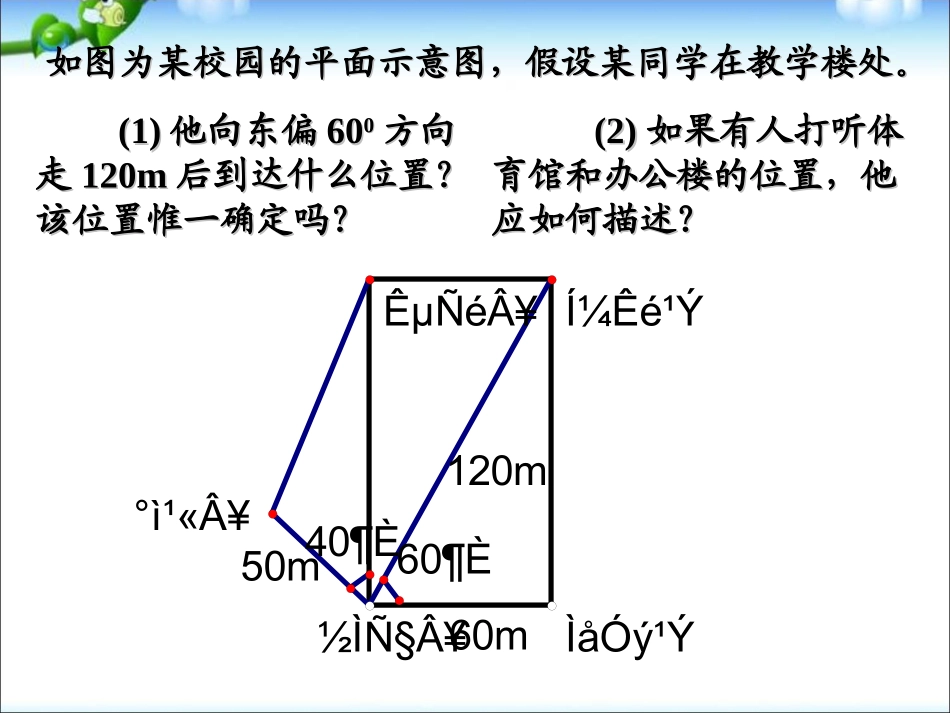
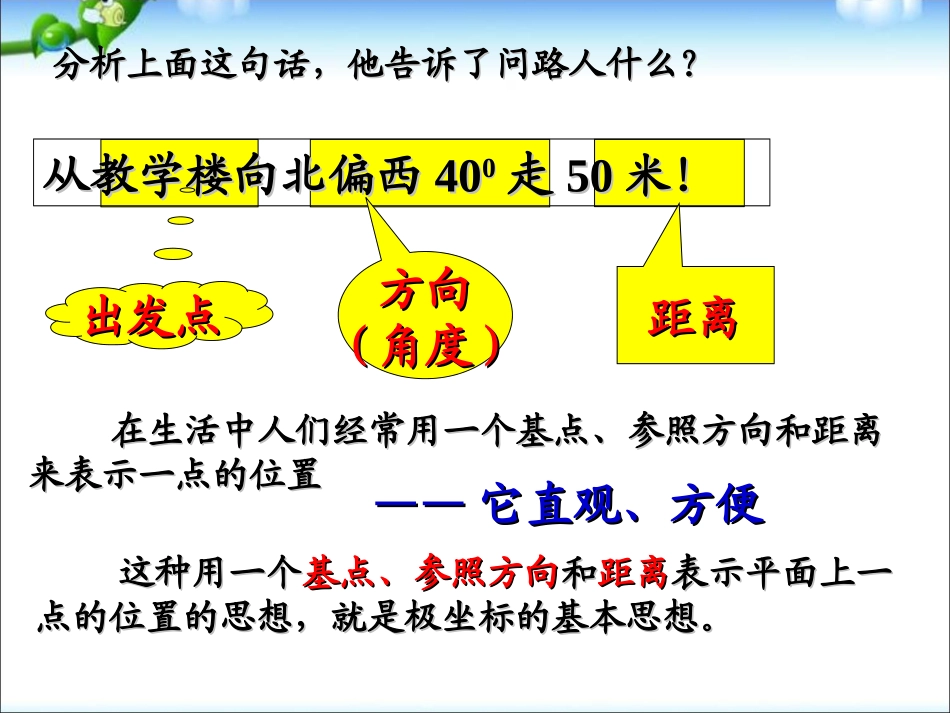
第一讲坐标系第一讲坐标系极坐标系极坐标系60m120m50m60¶È40¶ÈÌåÓý¹ÝͼÊé¹ÝʵÑéÂ¥°ì¹«Â¥½Ìѧ¥如图为某校园的平面示意图，假设某同学在教学楼处。如图为某校园的平面示意图，假设某同学在教学楼处。(2)(2)如果有人打听体如果有人打听体育馆和办公楼的位置，他育馆和办公楼的位置，他应如何描述？应如何描述？(1)(1)他向东偏他向东偏606000方向方向走走120m120m后到达什么位置？后到达什么位置？该位置惟一确定吗？该位置惟一确定吗？从教学楼向北偏西从教学楼向北偏西404000走走5050米！米！出发点出发点方向方向（角度）（角度）距离距离在生活中人们经常用一个基点、参照方向和距离在生活中人们经常用一个基点、参照方向和距离来表示一点的位置来表示一点的位置这种用一个这种用一个基点、参照方向基点、参照方向和和距离距离表示平面上一表示平面上一点的位置的思想，就是极坐标的基本思想。点的位置的思想，就是极坐标的基本思想。————它直观、方便它直观、方便分析上面这句话，他告诉了问路人什么？分析上面这句话，他告诉了问路人什么？XXOO极坐标系的概念：极坐标系的概念：在平面内取一个定点在平面内取一个定点OO，叫做，叫做极点极点。。自极点引一条射线自极点引一条射线OXOX，叫做，叫做极轴极轴。。再选定一个长度单位和再选定一个长度单位和角度单位角度单位（一般用（一般用弧度弧度制制））及及它的正方向它的正方向（通常取（通常取逆时针逆时针方向）。方向）。这样就建立了一个这样就建立了一个极坐标系极坐标系。。XXOOMM极坐标的表示方法极坐标的表示方法::对于极坐标平面上任意一点对于极坐标平面上任意一点M:M:表示线段表示线段OMOM的长度，叫做点的长度，叫做点MM的的极径极径;;表示以表示以OXOX为始边，射线为始边，射线OMOM为为终边的角终边的角,,叫做点叫做点MM的的极角极角;;有序数对有序数对((,,))就叫做点就叫做点MM的的极坐标极坐标。。特别强调：特别强调：表示线段表示线段OMOM的的长度长度，即点，即点MM到极点到极点OO的距离；的距离；表示从表示从OXOX到到OMOM的的角度角度，即以，即以OXOX（极（极轴）为始边，轴）为始边，OMOM为终边的角。为终边的角。不做特殊说明时不做特殊说明时,,≥0,≥0,R∈R∈当当MM在极点时，极坐标在极点时，极坐标=0=0，，可以取可以取任意值任意值。。ABCDEFGOX46535342例例11说说出下图中各点的极出下图中各点的极坐标坐标标出标出(2,π/6),(2,π/6),(4,3π/4),(4,3π/4),(3.5,5π/3)(3.5,5π/3)所在位置。所在位置。ABCDEFGOX46535342)3,6(),2,4(),65,3(QPHHPQ练习:在图中标出点一般地，不作特别说明，我们认为一般地，不作特别说明，我们认为≥≥00，，可以取任意实数。可以取任意实数。约定：极点的极坐标是约定：极点的极坐标是=0=0，可以取任意角。，可以取任意角。建立了极坐标后，给定建立了极坐标后，给定ρρ、、，就可以在平面，就可以在平面内惟一确定点内惟一确定点MM，，反过来，给定平面内任意一点，也可以找到反过来，给定平面内任意一点，也可以找到它的极坐标它的极坐标((，，))。。点与它的极坐标是否一一对应？点与它的极坐标是否一一对应？0,R)37,6(),311,6(),35,6(),3,6(在同一极坐标系中在同一极坐标系中,,有如下极坐标：有如下极坐标：这些极坐标之间有何异同？这些极坐标之间有何异同？极径相同极径相同，极角不同。，极角不同。这些极角有何关系？这些极角有何关系？极角的始边相同，终边也相同，极角的始边相同，终边也相同，即即::它们是它们是终边相同的角终边相同的角。。这些极坐标所表示的点有什么关系这些极坐标所表示的点有什么关系??它们表示同一个点。它们表示同一个点。XXOOMM点的极坐标的统一表达式点的极坐标的统一表达式::,,2kkZ极坐标与极坐标与表示同一个点。表示同一个点。一般地：一般地：平面内点的极坐标有无数种表示。平面内点的极坐标有无数种...