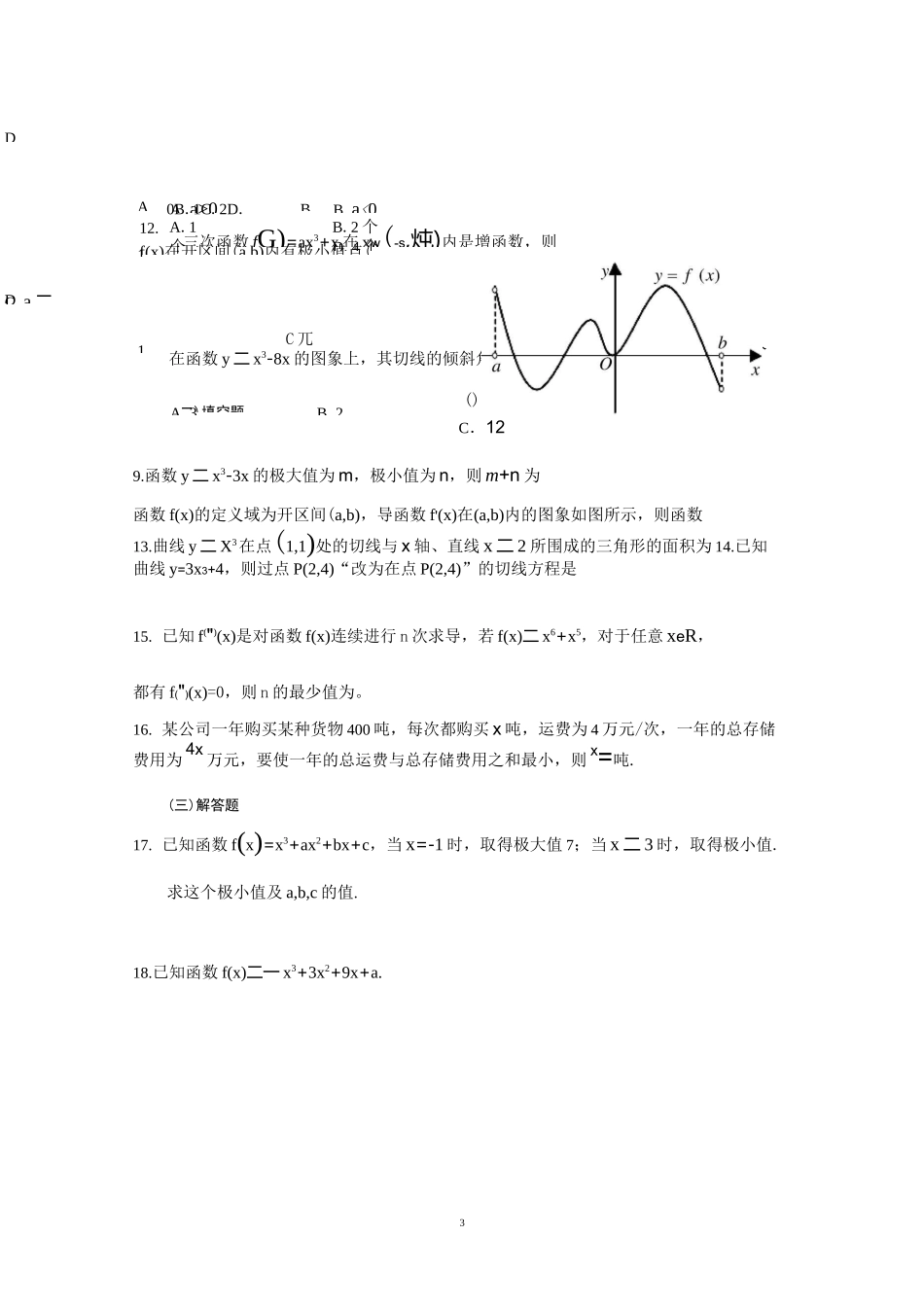
1专题 8:导数(文)经典例题剖析考点一:求导公式。例 1.f'(x)是 f(x)=3X3+2x+1 的导函数,则 f'(—1)的值是。考点二:导数的几何意义。例 2.已知函数 y=f(x)的图象在点 M(1,f(1))处的切线方程是 y=2x+2,则 f(1)+f'(1)=。例 3.曲线 y=x3-2x2-4x+2在点(1,一 3)处的切线方程是。考点三:导数的几何意义的应用。例 4.已知曲线 C:y 二 x3一 3x2+2x,直线 l:y=kx,且直线 l 与曲线 C 相切于点G。,y。)xo丰 0,求直线 1 的方程及切点坐标。考点四:函数的单调性。例 5.已知 fax3+3x2—x+1 在 R 上是减函数,求 a 的取值范围。考点五:函数的极值。例 6.设函数 f(x)二 2x3+3ax2+3bx+8c 在 x=1 及 x=2 时取得极值。(1)求 a、b 的值;(2)若对于任意的 xe[0,3],都有 f(x)0B.a<0C.a 二D1C 兀在函数 y 二 x3-8x 的图象上,其切线的倾斜角小于丁的点中,4()C.1坐标为整数的点的个A.3B.2D.012.f(x)在开区间(a,b)内有极小值点(A.1个C.3B.2 个D.4 个二)填空题C.12...