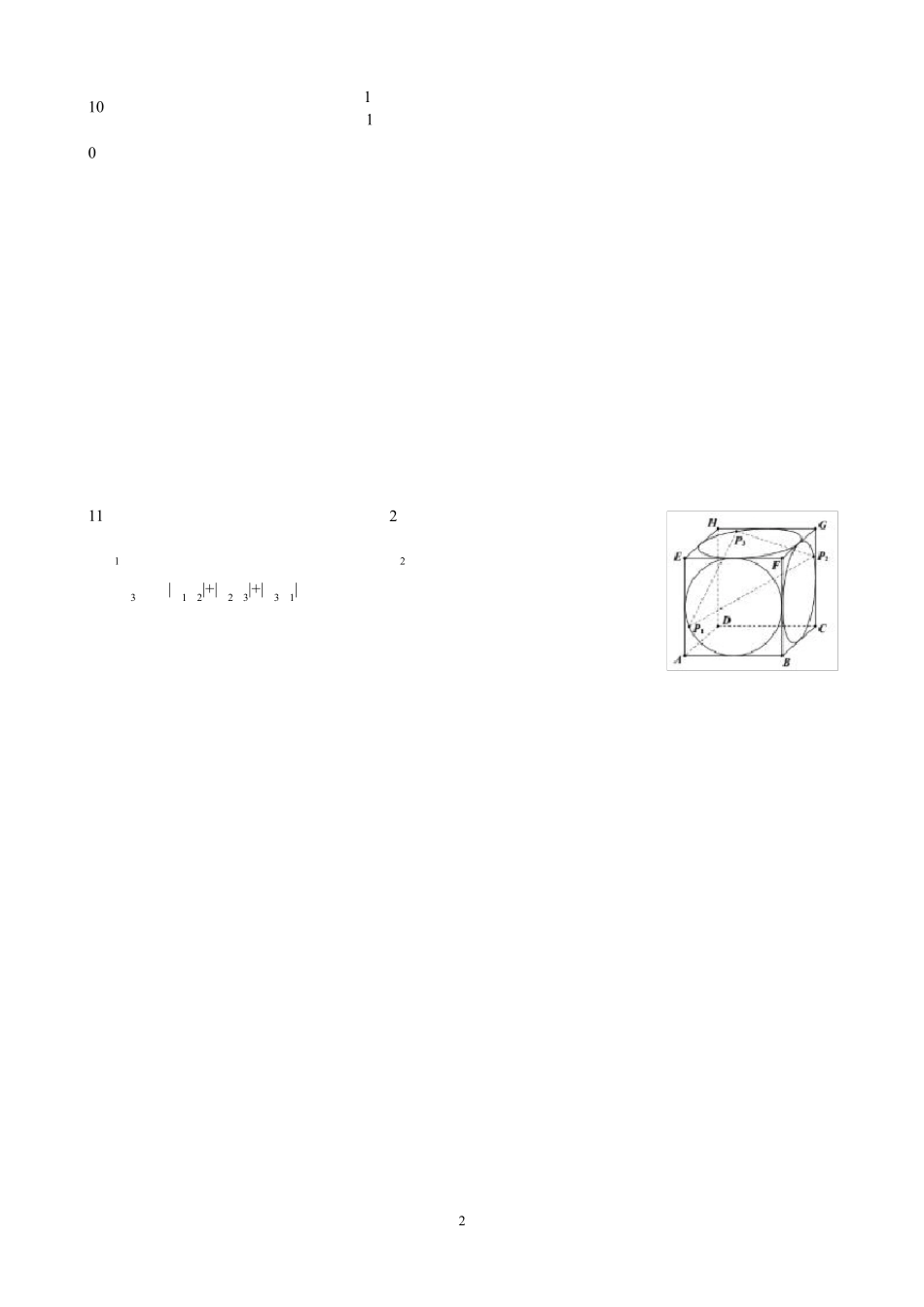
12021 年全国中学生数学奥林匹克竞赛(初赛)暨 2021 年全国高中数学联合竞赛一试(A 卷)一、填空题:本大题共 8 小题,每小题 8 分,满分 64 分.1.等差数列{an}满足 a2021=a20+a21=1,则 a1 的值为__________.2.设集合 A={1,2,m},其中 m为实数.令 B={a2|a∈A},C=A∪B.若 C的所有元素之和为 6,则C的所有元素之积为__________.3.设函数 f(x)满足:对任意非零实数 x,均有 f(x)=f(1)·x+2fx -1,则 f(x)在(0,+∞ )上的最小值为__________.4.设函数 f(x)=cosx+log2x(x>0),若正实数 a满足 f(a)=f(2a),则 f(2a)-f(4a)的值为__________.5.在△ABC中,AB=1,AC=2,B-C= 23,则△ABC的面积为__________.6.在平面直角坐标系 xOy中,抛物线Γ:y2=2px(p>0)的焦点为 F,过Γ上一点 P(异于 O)作Γ的切线,与 y轴交于点 Q.若|FP|=2,|FQ|=1,则向量 OP与 OQ的数量积为__________.7.一颗质地均匀的正方形骰子,六个面上分别标有点数 1,2,3,4,5,6.随机地抛掷该骰子三次(各次抛掷结果相互独立),所得的点数依次为 a1,a2,a3,则事件“|a1-a2|+|a2-a3|+|a3-a1|=6”发生的概率为__________.8.设有理数 r= pq∈(0,1),其中 p,q为互素的正整数,且 pq整除 3600.这样的有理数 r的个数为__________.二、解答题:本大题共 3 小题,满分 56 分.解答应写出文字说明、证明过程或演算步骤.9.已知复数列{zn}满足:z1=32 ,zn+1=nz(1+zni)(n=1,2,… ),其中i为虚数单位.求z2021的值.210.在平面直角坐标系中,函数y=11xx 的图像上有三个不同的点位于直线l上,且这三点的横坐标之和为0.求l的斜率的取值范围.11.如图,正方体ABCD-EFGH的棱长为2,在正方形ABFE的内切圆上任取一点P1,在正方形BCGF的内切圆上任取一点P2,在正方形EFGH的内切圆上任取一点P3.求|P1P2|+|P2P3|+|P3P1|的最小值与最大值.32021 年全国中学生数学奥林匹克竞赛(初赛)暨 2021 年全国高中数学联合竞赛一试(A 卷)一、填空题:本大题共 8 小题,每小题 8 分,满分 64 分.1.等差数列{an}满足 a2021=a20+a21=1,则 a1 的值为__________.【答案】19814001【解析】2.设集合 A={1,2,m},其中 m为实数.令 B={a2|a∈A},C=A∪B.若 C的所有元素之和为 6,则C的所有元素之积为__________.【答案】-8【...