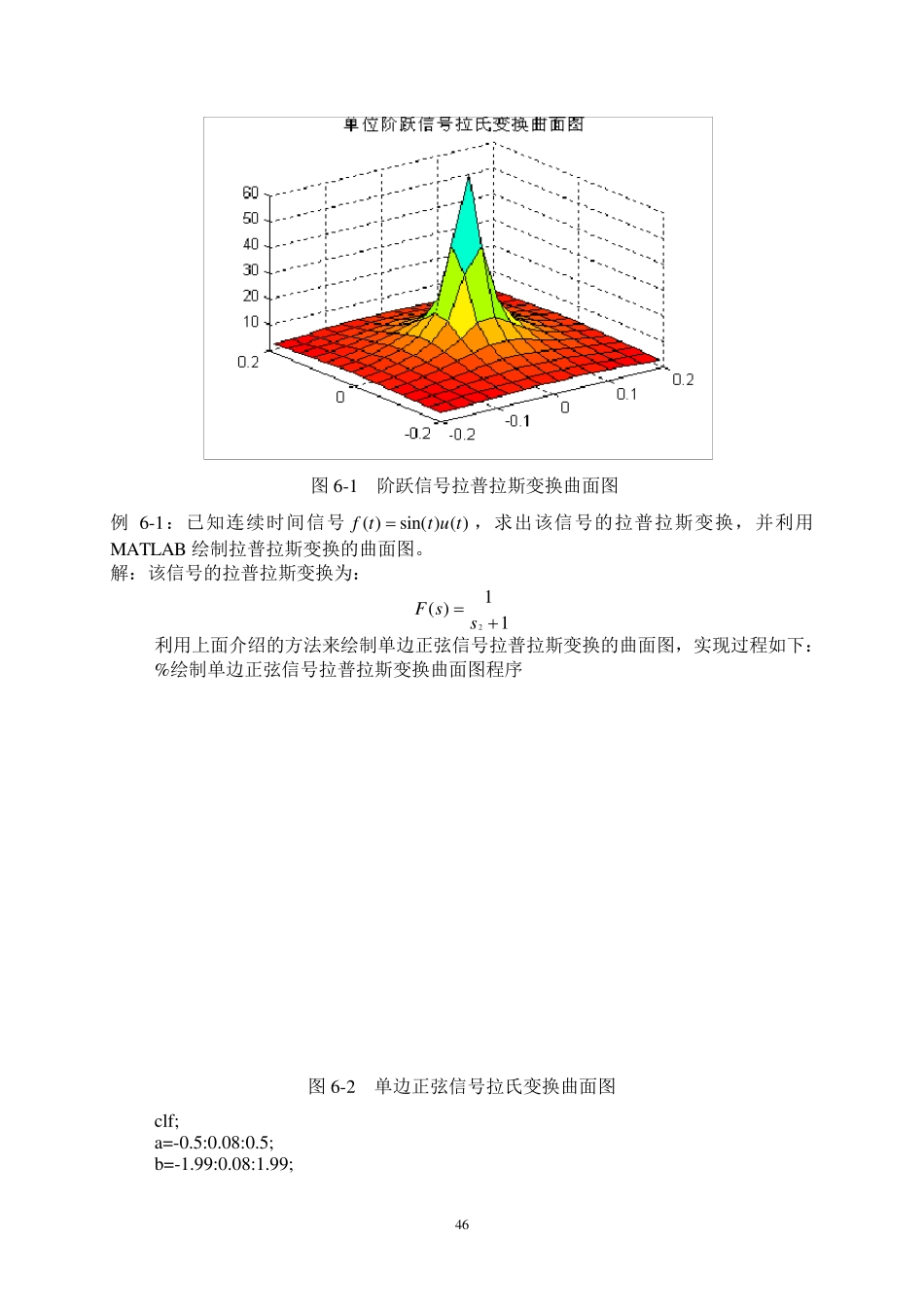
45 实验六 拉普拉斯变换及其逆变换 一、目的 (1)掌握连续系统及信号拉普拉斯变换概念 (2)掌握利用 MATLAB 绘制系统零极点图的方法 (3)掌握利用 MATLAB 求解拉普拉斯逆变换的方法 二、拉普拉斯变换曲面图的绘制 连续时间信号)(tf的拉普拉斯变换定义为: 0)()(dtetfsFst (6-1) 其中js,若以 为横坐标(实轴), j为纵坐标(虚轴),复变量 s 就构成了一个复平面,称为 s 平面。 显然,)(sF是复变量 s 的复函数,为了便于理解和分析)(sF随 s 的变化规律,可以将)(sF写成: )()()(sjesFsF (6-2) 其中,)(sF称为复信号)(sF的模,而)(s则为)(sF的幅角。 从三维几何空间的角度来看,)(sF和)(s对应着复平面上的两个平面,如果能绘出它们的三维曲面图,就可以直观地分析连续信号的拉普拉斯变换)(sF随复变量 s 的变化规律。 上述过程可以利用 MATLAB 的三维绘图功能实现。现在考虑如何利用 MATLAB 来绘制 s 平面的有限区域上连续信号)(tf的拉普拉斯变换)(sF的曲面图,现以简单的阶跃信号)(tu为例说明实现过程。 我们知道,对于阶跃信号)()(tutf,其拉普拉斯变换为ssF1)(。首先,利用两个向量来确定绘制曲面图的 s 平面的横、纵坐标的范围。例如可定义绘制曲面图的横坐标范围向量 x 1 和纵坐标范围向量 y 1 分别为: x 1=-0.2:0.03:0.2; y 1=-0.2:0.03:0.2; 然后再调用 meshgrid()函数产生矩阵 s,并用该矩阵来表示绘制曲面图的复平面区域,对应的 MATLAB 命令如下: [x ,y ]=meshgrid(x 1,y 1); s=x +i*y ; 上述命令产生的矩阵 s 包含了复平面2.02.0, 2.02.0j范围内以时间间隔 0.03 取样的所有样点。 最后再计算出信号拉普拉斯变换在复平面的这些样点上的值,即可用函数 mesh()绘出其曲面图,对应命令为: fs=abs(1./s); mesh(x ,y ,fs); su rf(x ,y ,fs); title('单位阶跃信号拉氏变换曲面图'); colormap(hsv ); ax is([-0.2,0.2,-0.2,0.2,0.2,60]); rotate3d; 执行上述命令后,绘制的单位阶跃信号拉普拉斯变换曲面图如图 6-1 所示。 46 例6-1:已知连续时间信号)()sin()(tuttf,求出该信号的拉普拉斯变换,并利用MATLAB 绘制拉普拉斯变换的曲面图。 解:该信号的拉普拉斯变换为: 11)(2 ssF 利用上面介绍的方法来绘制单边正弦信号拉普拉斯变换的曲面图,实现过程如下: %绘制单...