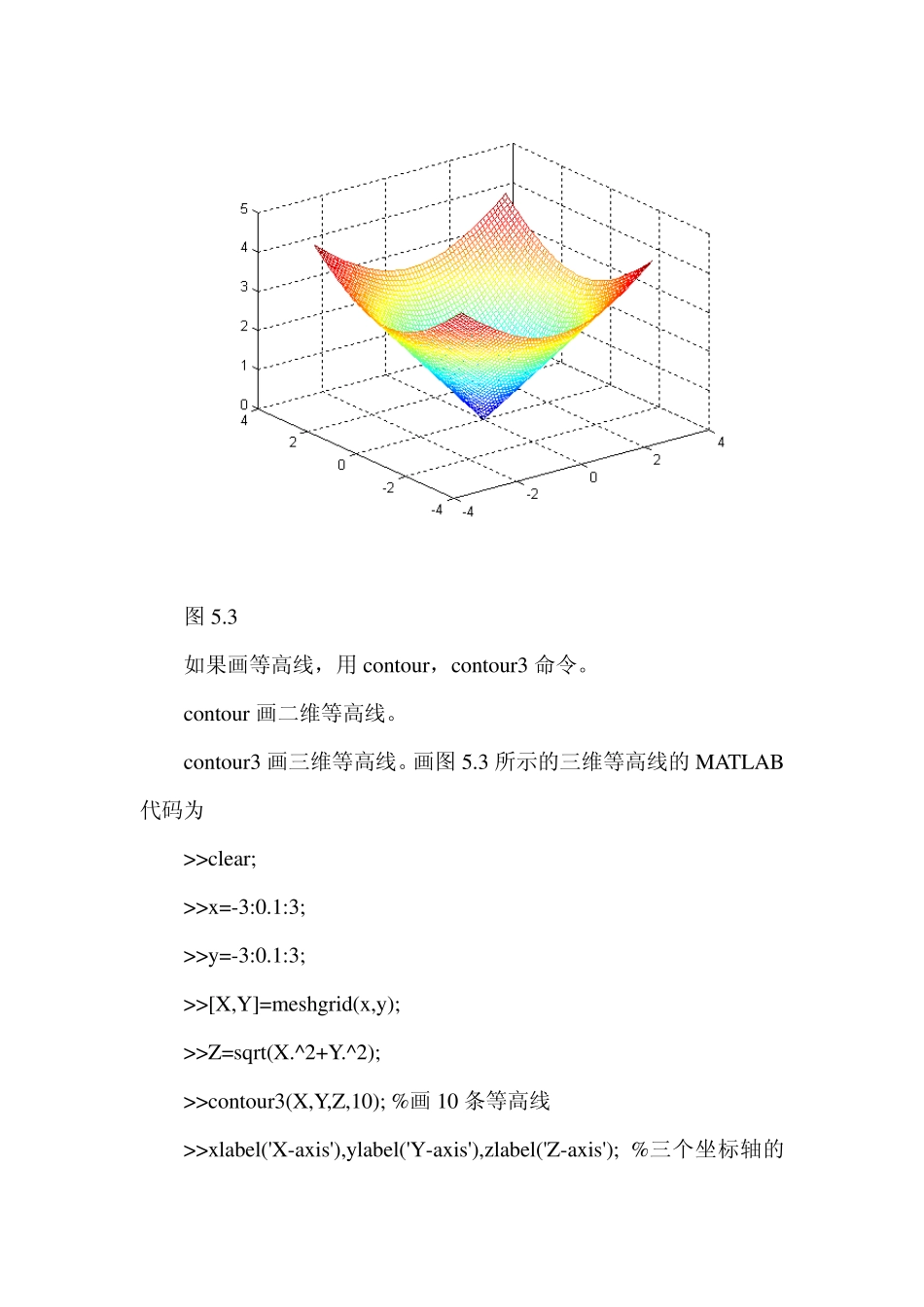
MATLAB 绘制二元函数的图形 【实验目的】 1.了解二元函数图形的绘制。 2.了解空间曲面等高线的绘制。 3.了解多元函数插值的方法。 4.学习、掌握 MATLAB 软件有关的命令。 【实验内容】 画出函数22yxz的图形,并画出其等高线。 【实验准备】 1.曲线绘图的MATLAB 命令 MATLAB 中主要用 mesh,surf 命令绘制二元函数图形。主要命令 mesh(x,y,z)画网格曲面,这里 x,y,z 是数据矩阵,分别表示数据点的横坐标,纵坐标和函数值,该命令将数据点在空间中描出,并连成网格。 surf(x,y,z)画完整曲面,这里 x,y,z 是数据矩阵,分别表示数据点的横坐标,纵坐标和函数值,该命令将数据点所表示曲面画出。 【实验重点】 1. 二元函数图形的描点法 2. 曲面交线的计算 3. 地形图的生成 【实验难点】 1. 二元函数图形的描点法 2. 曲面交线的计算 【实验方法与步骤】 练习1 画出函数22yxz的图形,其中]3,3[]3,3[),(yx。用 MATLAB 作图的程序代码为 >>clear; >>x =-3:0.1:3; %x 的范围为[-3,3] >>y =-3:0.1:3; %y 的范围为[-3,3] >>[X,Y]=meshgrid(x ,y ); %将向量 x ,y 指定的区域转化为矩阵 X,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值 Z >>mesh(X,Y,Z) 运行结果为 图5.3 如果画等高线,用contour,contour3 命令。 contour 画二维等高线。 contour3 画三维等高线。画图5.3 所示的三维等高线的 MATLAB代码为 >>clear; >>x=-3:0.1:3; >>y=-3:0.1:3; >>[X,Y]=meshgrid(x,y); >>Z=sqrt(X.^2+Y.^2); >>contour3(X,Y,Z,10); %画10 条等高线 >>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis'); %三个坐标轴的标记 >>title('Contou r3 of Su rface') %标题 >>grid on %画网格线 运行结果为 图 5.4 如果画图 5.4 所示的二维等高线,相应的 MATLAB 代码为 >>clear;x =-3:0.1:3;y =-3:0.1:3; >>[X,Y]=meshgrid(x ,y );Z=sqrt(X.^2+Y.^2); >>contou r (X,Y,Z,10); >>x label('X-ax is'),y label('Y-ax is'); >>title('Contou r3 of Su rface') >>grid on 运行结果为 如果要画 z=1 的等高线,相应的 MATLAB 代码为 >>clear;x=-3:0.1:3;y=-3:0.1:3; >>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2); >>contour(X,Y,Z,[1 1]) 运行结果为 练习2 二次曲面的方程如下 222222xyzdabc 讨论参数a,b,c 对其形状的...