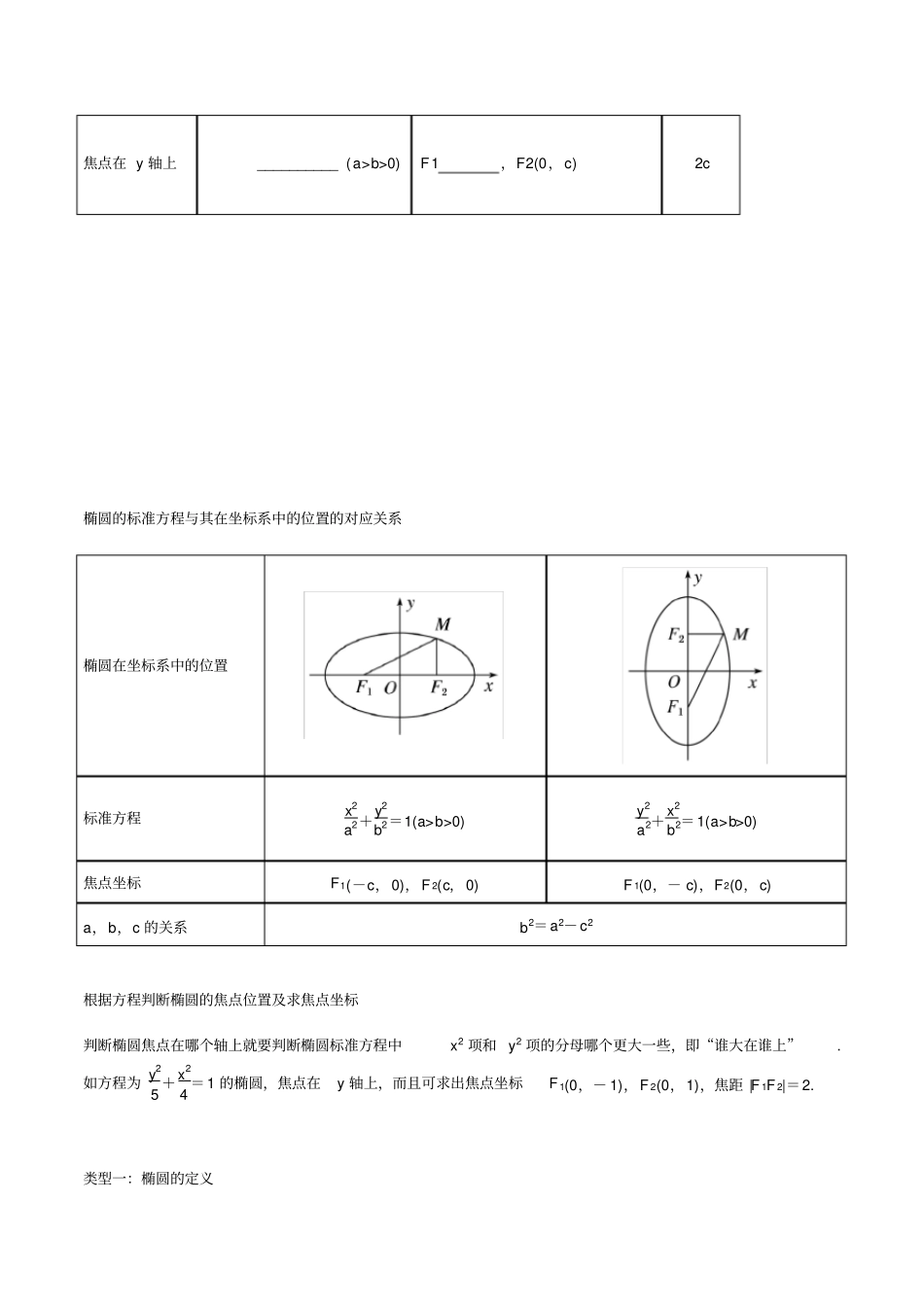
椭圆标准方程【知识点】知识点一椭圆的定义(1)我们把平面内与两个定点F1,F2 的距离的和等于常数(大于 |F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距. (2)椭圆的定义用集合语言叙述为:P={M||MF1|+ |MF2|=2a, 2a>|F1F2|}. (3)2a 与|F1F2|的大小关系所确定的点的轨迹如下表:条件结论2a>|F 1F2|动点的轨迹是椭圆2a=|F1F2|动点的轨迹是线段F1F22a<|F 1F2|动点不存在,因此轨迹不存在【问题一】在椭圆的标准方程中a>b>c 一定成立吗?不一定,只需a>b,a>c 即可, b, c 的大小关系不确定【问题二】若两定点A、B 间的距离为6,动点 P 到两定点的距离之和为10,如何求出点P 的轨迹方程?以两定点的中点为坐标原点,以AB 所在直线为x 轴建立直角坐标系,则A(3 ,0),B(- 3,0).设 P(x,y),依题意得 |PA|+|PB|=10,所以x-32+y2+x+32+y2= 10,即点 P 的轨迹方程为 x225+ y216=1. 椭圆标准方程的两种形式焦点位置标准方程焦点焦距焦点在 x 轴上 _________ (a>b>0)F1(-c,0), F2______2c焦点在 y 轴上 __________ (a>b>0)F1 ,F2(0,c)2c椭圆的标准方程与其在坐标系中的位置的对应关系椭圆在坐标系中的位置标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0)焦点坐标F1(-c,0),F 2(c,0)F 1(0,- c),F2(0,c)a,b,c 的关系b2=a2-c2根据方程判断椭圆的焦点位置及求焦点坐标判断椭圆焦点在哪个轴上就要判断椭圆标准方程中x2 项和 y2 项的分母哪个更大一些,即“谁大在谁上”.如方程为 y25+x24=1 的椭圆,焦点在y 轴上,而且可求出焦点坐标F 1(0,- 1),F 2(0,1),焦距 |F 1F 2|=2. 类型一:椭圆的定义【例 1】点 P(-3,0)是圆 C: x2+y2-6x-55=0 内一定点,动圆M 与已知圆相内切且过P 点,判断圆心M 的轨迹 . 【变式】若将本例中圆C 的方程改为: x2+y 2-6x=0 且点 P(-3,0)为其外一定点,动圆M 与已知圆 C 相外切且过 P 点,求动圆圆心M 的轨迹方程 . 即x- 3 2+ y-0 2-x+3 2+ y-0 2= 3,整理得 x294- y2274=1(x<0). 方程 x2+y2-6x-55= 0 化标准形式为: (x-3)2+y2=64,圆心为 (3,0),半径 r=8.因为动圆 M 与已知圆相内切且过P 点,所以 |MC |+|MP |=r=8,根据椭圆的定义,动点M 到两定点C,P 的距离之和为定值8>6=|CP|,所以动点M 的轨迹...