§13怎样计算磁感应强度VIP免费

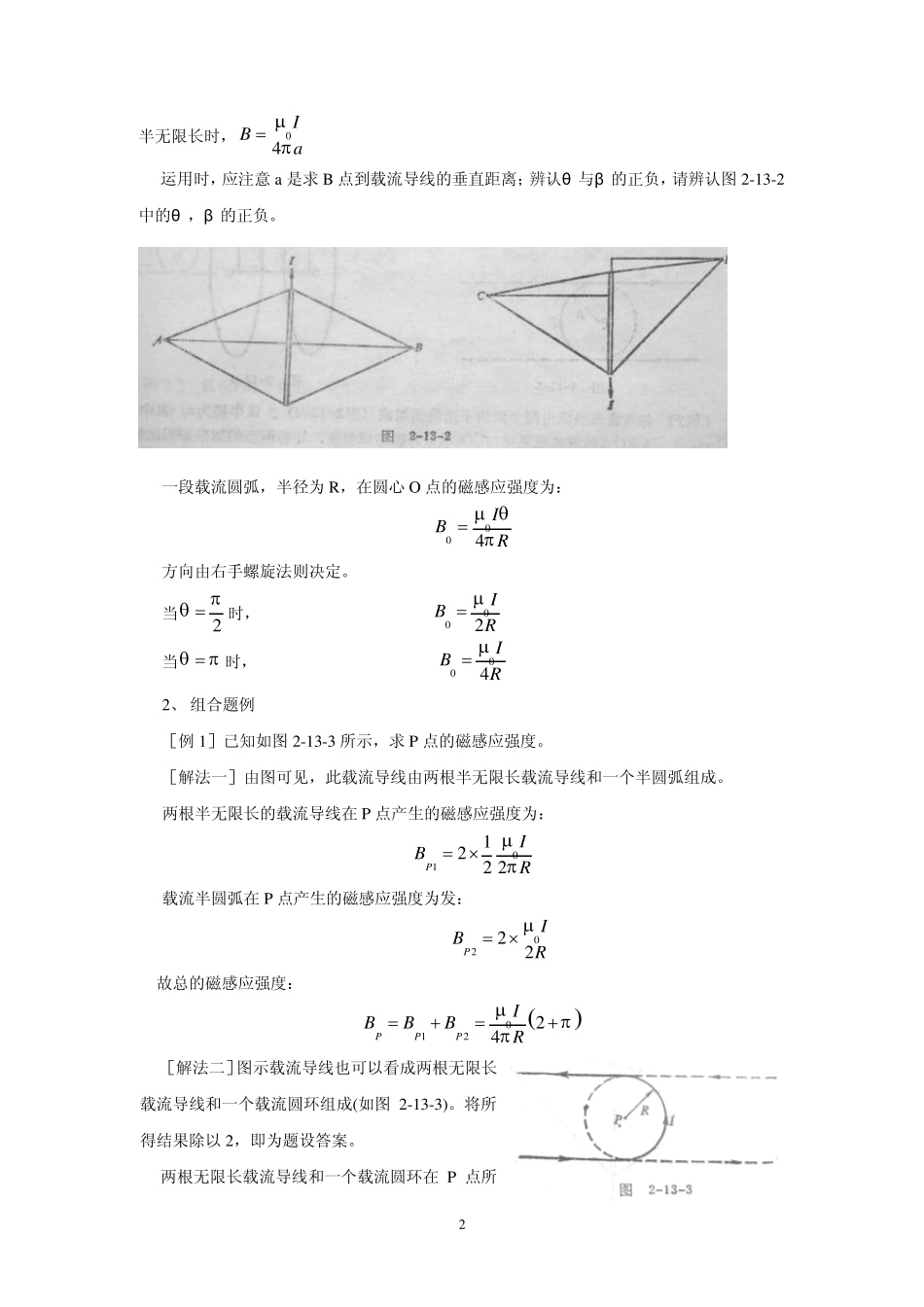
1 §1 3 怎 样 计 算 磁 感 应强度 在稳恒磁场中的磁感应强度，可用毕奥-沙伐尔定律和安培环路定律来求解。 毕奥-沙伐尔定律在成块中的地位，好像静电场中的库仑定律一样，是很重要的。它是计算磁感应强度最普遍、最基本的方法。安培环路定律，是毕奥 -沙伐尔定律的基础上加上载流导线无限长等条件而推导出来的。困此，用安培环路定律遇到较大的限制。但是，有一些场合，应用安培环路定律往往给我们带来不少方便。 一、用毕奥-沙伐尔定律计算 真空中有一电流元 Idl ，在与它相距 r处的地方所产生的磁感应强度 dB ，由毕奥-沙伐尔定律决定。 03(1)4IdlrdBr 式中，r是由电流元 Idl 指向求 B 点的距离矢量。式(1)是矢量的矢积，故dB 垂直于dl与 r组成的平面，而且服从右手螺旋法则。真空的磁导率70410/H m。 B 是一个可叠加的物理量，因此，对于一段(弯曲的或直的)载流导线 L 所产生的 B 磁感应强度为： 03(2)4LIdlrBr 1、 基本题例 在磁场的计算中，许多习题是载流直导线和圆弧导线不同组合而成的。因此，必须熟练掌握一段载流的长直导线和一段载流的圆弧导线的磁场的计算公式。 图2-13-1 所示为一段长直载流导线，它的磁感应强度的计算公式为： 012coscos4Ba 或： 021coscos4Ba 当载流直导线“无限长”时，02IBa； 2 半无限长时， 04IBa 运用时，应注意a是求B 点到载流导线的垂直距离；辨认θ 与β 的正负，请辨认图2-13-2中的θ ，β 的正负。 一段载流圆弧，半径为R，在圆心O 点的磁感应强度为： 004IBR  方向由右手螺旋法则决定。 当2 时， 002IBR 当时， 004IBR 2、 组合题例 ［例 1］已知如图2-13-3 所示，求P 点的磁感应强度。 ［解法一］由图可见，此载流导线由两根半无限长载流导线和一个半圆弧组成。 两根半无限长的载流导线在P 点产生的磁感应强度为： 01122 2PIBR 载流半圆弧在P 点产生的磁感应强度为发： 0222PIBR 故总的磁感应强度： 01224PPPIBBBR ［解法二］图示载流导线也可以看成两根无限长载流导线和一个载流圆环组成(如图2-13-3)。将所得结果除以 2，即为题设答案。 两根无限长载流导线和一个载流圆环在P 点所 3 产生的磁感应强度分别为022IR和02IR，它们的和被2 除，即得与解法一相同...