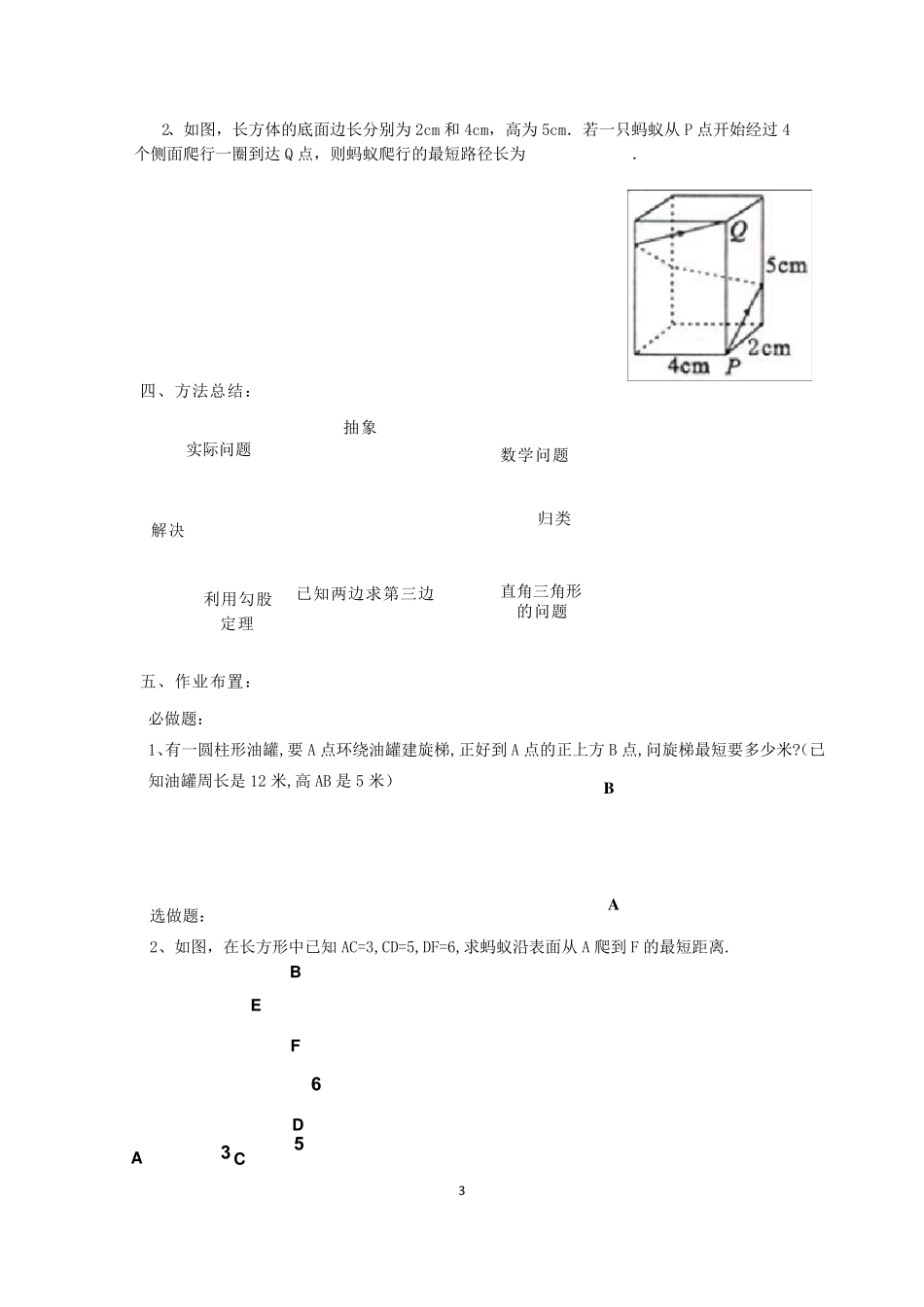
1 A C B A B A B §14.2 勾股定理的应用---最短路径问题 安海中学 谢伟良 教学目标: 知识与技能目标:能运用勾股定理解决简单的实际问题. 过程与分析目标:经历勾股定理的应用过程,熟练掌握其应用方法,明确应用的条件. 情感与态度目标:培养合情推理能力,体会数形结合的思维方法,激发学习热情 教学重点:利用“两点之间线段最短”和“勾股定理”求得最短路程. 教学难点:寻找最短路径. 教学关键:把立体图形转化为合适的平面图形寻得最短路径再构造直角三角形应用勾股定理求最短路程. 教学准备: 教师准备:幻灯片、直尺. 学生准备:复习勾股定理,自制圆柱体、立方体和长方体. 教学过程: 一、复习引入,创设情境 1.复习提问:线段性质定理、勾股定理的内容及数学式子表示. 设定情景引入新课. 2.情景设定 1(投影出示): 二、创设情境,解决问题 情景设定 2: 在一款长 30cm 宽40cm 的砧板上,蚂蚁要从点 A 处到点 B 处觅食,试问这只蚂蚁要 怎么选择路线才能使路线最短?最短距离是多少? 如图所示,圆柱体的底面直径为 6cm,高为 12cm,一只蚂蚁从A 点出发,沿着圆柱的侧面爬行到点 B,试求出爬行的最短路程(π取3). 22BCAC ∴爬行的最短路程约为 15cm。 在Rt△ABC 中, ∠C=90º ∴ )(5040302222cmBCACAB∴ 走线段 AB 的路线最短,且最短距离为 50cm. 解:如图, 在Rt△ABC 中, ∠ACB=90° BC=½πd≈½×3×6=9cm, ∴AB= 22912)(15 cm 2 A B 1 3 2 A B 2 0.3 0.2 B 情景设定3: 变式训练: 如果把圆柱换成棱长为10cm 的正方体盒子,蚂蚁沿着表面从A 点爬行到B 点需要的最短路程 又是多少呢?想一想都有哪些爬行路径?需要经过哪些面? 如图示,有一个长为3cm,宽为2cm,高为1cm 的长方体,一只蚂蚁要沿着表面从A 到B 处觅食,请问需要爬行的最短路程是多少呢? 方法小结: 把几何体适当展开成平面图形,再利用“两点之间线段最短”和“勾股定理”来解决问题. 三、学以致用,巩固提升 1、如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A 和 B 是台阶上两个相对的顶点,A 点有一只蚂蚁,想到B 点去吃可口的食物,问蚂蚁沿着台阶爬行到B 点的最短路程是多少? A 3 实际问题 直角三角形 的问题 数学问题 利用勾股 定理 已知两边求第三边 抽象 归类 解决 A B 3 5 6 A C...