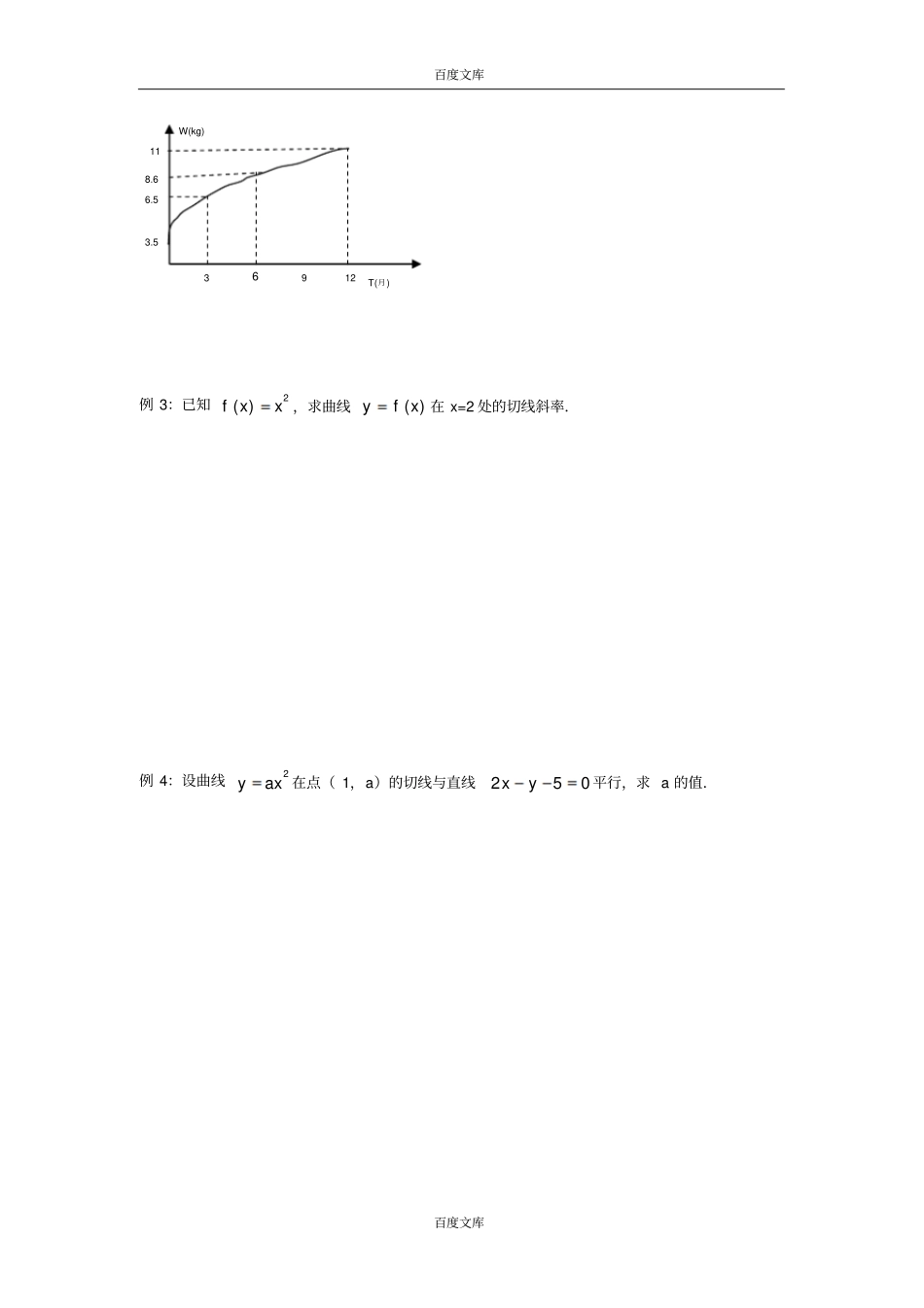
百度文库百度文库江苏省泰兴中学高二数学讲义(22)导数的概念( 1)【本课目标】1、了解函数平均变化率、瞬时变化率的概念,会求函数的平均变化率、瞬时变化率;2、理解平均变化率、瞬时变化率的几何意义、物理意义,会解决实际问题. 【重点难点】重点:平均变化率的含义,切线斜率的求法难点:割线逼近切线的“无限递近”的思想【预习导引】1、函数 y=x4-4x+3 在区间 [-2,3]上的平均变化率为_________. 2、函数xxf1)(在区间 [-2,-1]上的平均变化率为_________. 3、已知函数f(x)= x2-x 在区间 [1,t] 上的平均变化率为2,则 t=_________. 4、火箭发射时位移函数为s(t)=0.2t3+8t2+16t ,则第 2s 末的瞬时速度为_______. 【典型例题】例 1、(1)分别计算函数3( )f xx 在区间 [1 ,3] 、[1 ,2] 上的平均变化率;(2)已知函数xxxf2)(图象上 A(-1 ,-2 )及 B(-1+x ,-2+y ), 则________xy;(3)求函数1( )f xx在00[,]xxx (00x)的平均变化率. 例 2、某婴儿从出生到第12 个月的体重如图,试分别计算从出生到第3 个月以及第6 个月到第 12 个月该婴儿体重的平均变化率. 百度文库百度文库例 3:已知2( )f xx ,求曲线( )yf x 在 x=2 处的切线斜率.例 4:设曲线2yax 在点( 1,a)的切线与直线250xy平行,求 a 的值.T(月) W(kg) 6 3 9 12 3.5 6.5 8.6 11 百度文库百度文库【学后反思】1.平均变化率是曲线陡峭程度的“数量”化; 2.由割线运动来逼近切线,割线斜率逼近切线斜率是“以直代曲”的一种数量化.3.“无限趋近于”意指无限接近常数A,而且与常数A 的距离要多小,就有多小;“△ x 无限趋近于常数A”通常用符号“△x→A”表示.【巩固练习】1.①函数( )31f xx在区间 [ 1,1]上的平均变化率是________.②函数3( )g xx 在区间 [ 1,1]上的平均变化率是________.2.抛物线2yx 在点 P(1,-1)处的切线的斜率是_________.江苏省泰兴中学高二数学课后作业(22)班级 : 姓名 : 学号:【A 组题 】1.在区间 [m,n] 上,下列函数的平均变化率为定值的是A.2yxB.3yxC.1yxD.2yx2.一木块沿某一斜面自由下滑,测得下滑的水平距离s 与时间 t 之间的函数关系为218st ,则木块从 2s 到 4s 的平均速度是 ___________. 3.一辆汽车按规定234st做直线运动,则这辆汽车在t=3s 时的瞬时速度为______. 4.曲线2yx 在 x=0 处切线的斜率为_______...