剪力弯矩和分布荷载间的关系及应用VIP免费

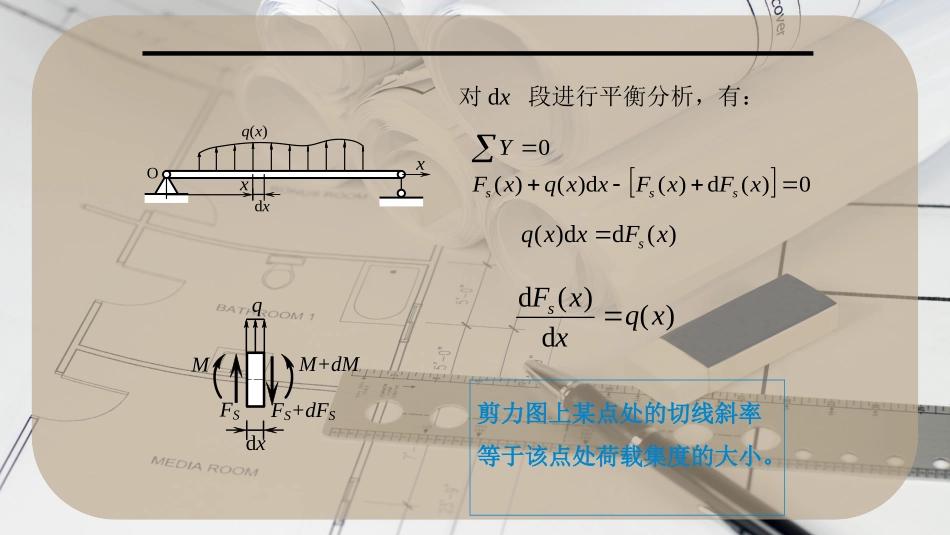
剪力、弯矩与分布荷载间的关系及应用工程力学剪力、弯矩与分布荷载间的关系及应用一、剪力、弯矩与分布荷载间的关系1、支反力：2qlFFBYAYLqFAYFBY2、内力方程qxqlxFs21)()0(lx22121)(qxqlxxM)0(lx3、讨论：)(21)(xFqxqldxxdMs)()(xqqdxxdFsx对dx段进行平衡分析，有：0)(d)(d)()(0xFxFxxqxFYsss)(dd)(xFxxqs剪力图上某点处的切线斜率等于该点处荷载集度的大小。xdxxOq(x)MFSdxFS+dFSM+dMq)(d)(dxqxxFs0)](d)([)())(d(21)d(,0)(2xMxMxMxxqxxFFmsiA弯矩图上某点处的切线斜率等于该点处剪力的大小。)(d)(dxFxxMsMFSdxFS+dFSM+dMq)(d)(d22xqxxM)(d)(dxqxxFs)(d)(dxFxxMs由，得二、微分关系的应用2、分布力q(x)=常数时——剪力图为一条斜直线；弯矩图为一条二次曲线。1、分布力q(x)=0时——剪力图为一条水平线；弯矩图为一条斜直线。Fs图：M图：（1）当分布力的方向向上时——剪力图为斜向上的斜直线；弯矩图为上凹的二次曲线。Fs图：M图：M(x))(d)(dxqxxFs)(d)(dxFxxMs)(d)(d22xqxxM4、集中力偶处——剪力图无变化；弯矩图有突变，突变值的大小等于集中力偶的大小。5、弯矩极值处——剪力为零的截面、集中力作用的截面、集中力偶作用的截面。3、集中力处——剪力图有突变，突变值等于集中力的大小；弯矩图有折角。（2）当分布力的方向向下时——剪力图为斜向下的斜直线；弯矩图为下凹的二次曲线。Fs图：M图：M(x)外力无分布荷载段均布载荷段集中力集中力偶q=0q>0q<0Fs图特征M图特征CFCm水平直线xFsFs>0FsFs<0x斜直线增函数xFsxFs降函数xFsCFs1Fs2Fs1–Fs2=F自左向右突变xFsC无变化斜直线Mx增函数xM降函数曲线xM盆状坟状xM自左向右折角自左向右突变xM折向与F同向三、剪力、弯矩与分布力之间关系的应用图MmMM12与m同xM1M2[例]用简易作图法画下列各图示梁的内力图。控制点:端点、分段点（外力变化点）和驻点（极值点）等。四、简易法作内力图法（利用微分规律）:利用内力和外力的关系及特殊点的内力值来作图的方法。基本步骤：1、确定支座反力；2、利用微分规律判断梁各段内力图的形状；3、确定控制点内力的数值大小及正负；4、描点画内力图。ABx1lFAyFBy(a)x2CFFD(b)FsxFFabcMx(c)Fl1dg1、确定支座反力2、剪力图将梁分为AB，BC，CD三段，梁上无分布载荷，各梁段为水平直线。利用截面法知：剪力图中以此画出a，b，c三点。过三点分别画出水平直线，得剪力图（图b）。3、弯矩图利用截面法，知：做出弯矩图中对应e,d,f,g四点，连接de，ef，fg得剪力图（图c）。FFFDyAyFFFFFSCSBSA,0,0,,011DCCBBAMFlMMFlMMM在BC段内，剪力为零，弯矩为常数。梁段的各横截面的弯矩为常数，剪力为零的受力状态，称为纯弯曲。1、确定支座反力2、剪力图讨论：梁分为AC，CB，BD三段。AC段：A处剪力突变到正72KN，由于q=0，AC段剪力图为水平直线；CB段：为向下倾斜直线，斜率为-20，到B处为-88KN；B处剪力图向上突变，突变值大小FBy到60KN。BD段：BD段斜率仍为-20，到D处变化为20KN。D处剪力向下突变F到坐标轴上，即可画出剪力图如图b所示。F=20kNM=160kNmA(a)Dq=20kN/mBC2m8mx2m5.6m72kN60kN20kN88kN(b)FsxkN148kN72ByAyFF，3、弯矩图C处有集中力偶，弯矩图在此处有向下跳跃间断点。AC处剪力为正常数，剪力图为向上倾斜直线。CB和BD段弯矩图为开口向下抛物线。作弯矩图需找控制点弯矩值由于CB段有剪力零点，此处弯矩有极值。得x=5.6m据此，可得弯矩图如图c所示。最大弯矩值在C点左侧，xM(c)16kNm80kNm113.6kNm144kNm0AMmkNMC144-mkNMC16mkNMMBB800-DM0)2(xqFFAySmkNM144max1）根据梁受力情况可以直接分段画剪力图，无需计算；2）弯矩图需要找个别控制点，根据规律就可以画出弯矩图；3）特别注意：剪力图为零的点，一般会出现弯矩极值。谢谢观看！工程力学