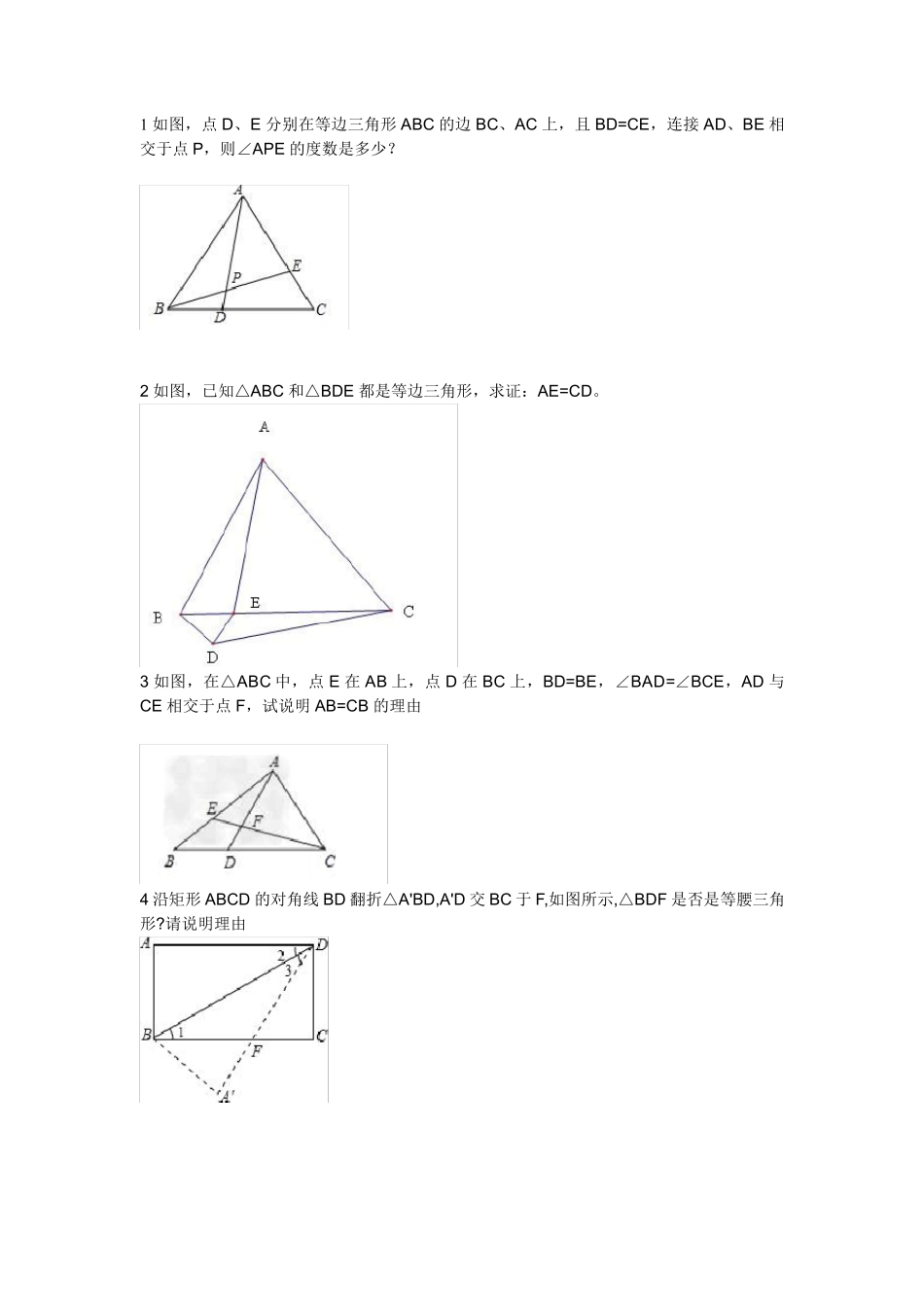
1 如图,点D、E 分别在等边三角形ABC 的边BC、AC 上,且BD=CE,连接AD、BE 相交于点P,则∠APE 的度数是多少?2 如图,已知△ABC 和△BDE 都是等边三角形,求证:AE=CD。3 如图,在△ABC 中,点E 在AB 上,点D 在BC 上,BD=BE,∠BAD=∠BCE,AD 与CE 相交于点F,试说明 AB=CB 的理由4 沿矩形ABCD 的对角线 BD 翻折△A'BD,A'D 交BC 于F,如图所示,△BDF 是否是等腰三角形?请说明理由5 如图,已知AB=AC,∠A=36°,AB 的中垂线 MN 交 AC 于点 D,交 AB 于点 M,求证:(1)BD 平分∠ABC ;(2)△BCD 为等腰三角形。6如图,△ACD 和△BCE 都是等腰直角三角形,∠ACD=∠BCE=90°,AE 交 CD 于点 F,BD 分别交 CE、AE 于点 G、H。试猜测线段 AE 和 BD 的数量和位置关系,并说明理由。7(1)如图,点 O 是线段 AD 的中点,分别以 AO 和 DO 为边在线段 AD 的同侧作等边三角形OAB 和等边三角形 OCD,连结 AC 和 BD,相交于点 E,连结 BC.求∠AEB 的大小;(2)如图,ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点 O 旋转(ΔOAB和ΔOCD 不能重叠),求∠AEB 的大小.8 如图1,在△ABC 中,AB=AC,AB 的垂直平分线交A 于N,交BC 的延长线于M,∠A=40°,求∠NMB 的大小。(1)如图1,在△ABC 中,AB=AC,AB 的垂直平分线交A 于N,交BC 的延长线于M,∠A=40°,求∠NMB 的大小。(2)如果将(1)中的∠A 的度数改为 70°(如图2),其余条件不变,再求∠NMB 的大小(3)你发现有什么样的规律性?试证明(4)将(1)中的∠A 改为钝角,对这个问题规律性的认识,是否需要加以修改?9 点 C 为线段 AB 上一点,△ACM、△CBN 是等边三角形,直线AN、MC 交于点 E,直线BM、CN交于点 F.(1)求证:AN=MB.(2)求证:△CEF 为等边三角形.10 已知如图,在四边形 ABCD 中AB=BC=CD=DA.E、F 分别是 BC、CD 上的点,且 CE=CF.①求证△ABE 全等于△ADF.②过点 C 作 CG∥EA 交AF 于H,交AD 于G.若∠BAE=25°,∠BCD=130°,求∠AHC 的度数已知如图,在四边形 ABCD 中AB=BC=CD=DA.E、F 分别是 BC、CD 上的点,且 CE=CF.①求证△ABE 全等于△ADF.②过点C 作CG∥EA 交AF 于H,交AD 于G.若∠BAE=25°,∠BCD=130°,求∠AHC 的度数11 已知:如图,锐角△ABC 的两条高 BD、CE 相交于点O,且 OB=OC.(1)求证:△ABC 是等腰三...