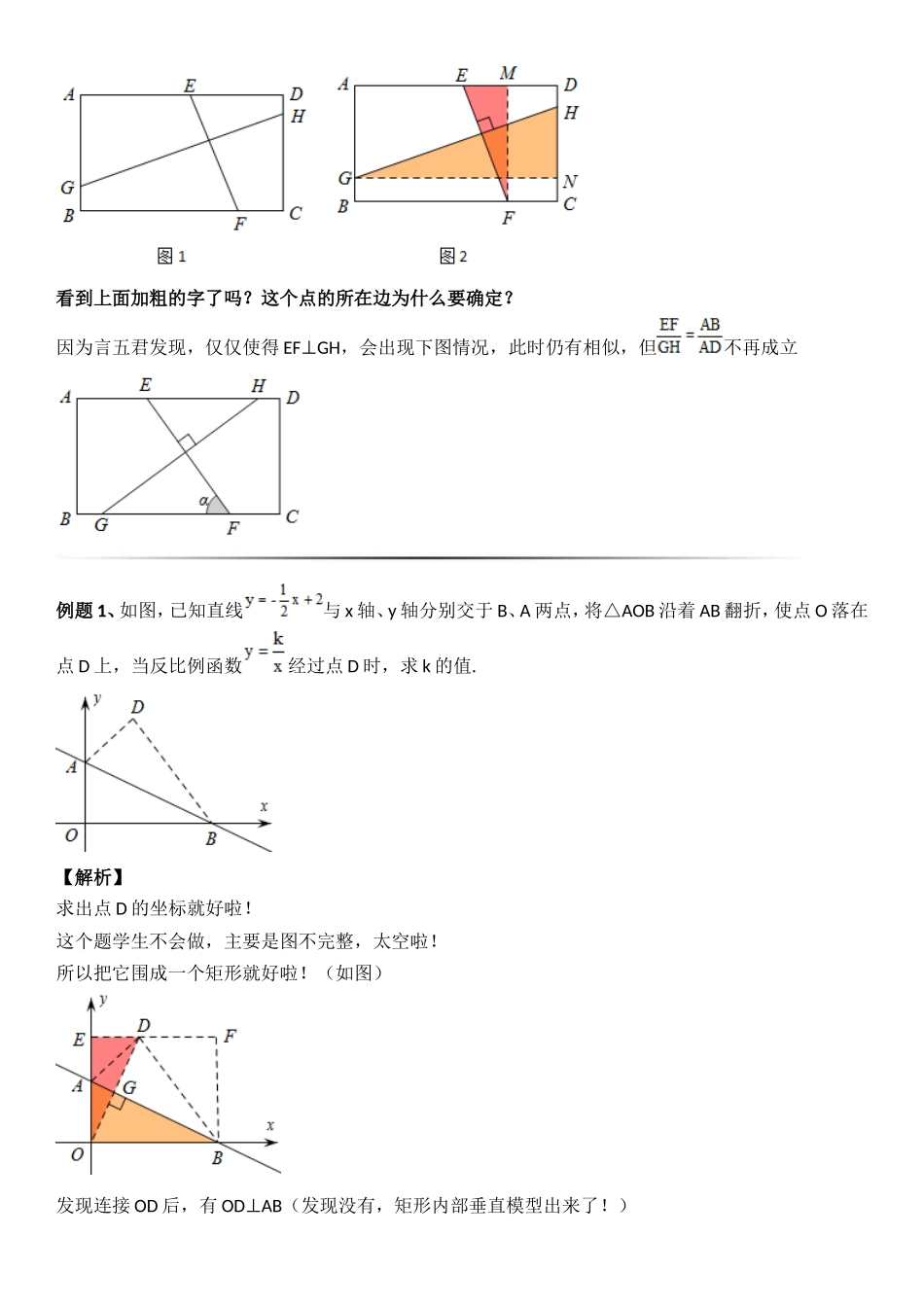
【正方形内的十字架结构】1、在正方形 ABCD 中,BN⊥AM,则常见的结论有哪些?2、在正方形 ABCD 中,E、F、G、H 分别为 AB、CD、BC、AD 边上的点,若 EF⊥GH,上述结论是否仍然成立?当然是仍然成立的,所以大体上思路是“从垂直可利用全等推导出相等”【思考】从相等是否可推导出垂直?3、在正方形 ABCD 中,E、F、G、H 分别为 AB、CD、BC、AD 边上的点,若 EF=GH,则 EF 与 GH 是否垂直,若不是,请画出反例.如图,垂直只是相等时的一种情况,另一种,只需使得AH’=DH,BG’=CG’即可作出 HG=H’G’利用上述结论,做题可就方便多了!例题 1、如图,将边长为 4 的正方形纸片 ABCD 折叠,使得点 A 落在 CD 的中点 E 处,折痕为 FG,点 F 在AD 边,求折痕 FG 的长;【解析】连接 AE,由轴对称的性质可知,AEFG⊥(应该是 FG 垂直平分 AE)这样就可以直接用上面的结论啦!所以由垂直得到相等,所以 FG=AE=【十字结构在矩形中】【思考】既然正方形内可出现垂直,那么矩形内出现垂直会有什么结论呢?1、如图,在矩形 ABCD 中,AB=m,AD=n,在 AD 上有一点 E,若 CEBD⊥,则CE 和 BD 之间有什么数量关系?这里面基本型较多,有相似里的直角母子型,又有 A 形相似,但是为了延续上面的探究我们要讲的模型是△CDEBCD∽△,证明较简单,不证了,记住这个结论所以即 CE 和 BD 之比等于矩形邻边之比2、如图 1,一般情况,在矩形 ABCD 中,E、F、G、H 分别为 AD、BC、AB、CD 边上的点,当 EFGH⊥时,有的结论,证明方法如图 2,证明△FMEGNH∽即可看到上面加粗的字了吗?这个点的所在边为什么要确定?因为言五君发现,仅仅使得 EFGH⊥,会出现下图情况,此时仍有相似,但不再成立例题 1、如图,已知直线与 x 轴、y 轴分别交于 B、A 两点,将△AOB 沿着 AB 翻折,使点 O 落在点 D 上,当反比例函数经过点 D 时,求 k 的值.【解析】求出点 D 的坐标就好啦!这个题学生不会做,主要是图不完整,太空啦!所以把它围成一个矩形就好啦!(如图)发现连接 OD 后,有 ODAB⊥(发现没有,矩形内部垂直模型出来了!)【练习】如图把边长为 AB=6,BC=8 的矩形 ABCD 对折,使点 B 和 D 重合,求折痕 MN 的长.请在 20 秒内快速求出此题答案 答案:【十字结构在直角三角形中】我们知道直角三角形是可以看成是连接矩形对角线后分成的图形所以矩形的结论可沿用至直角...