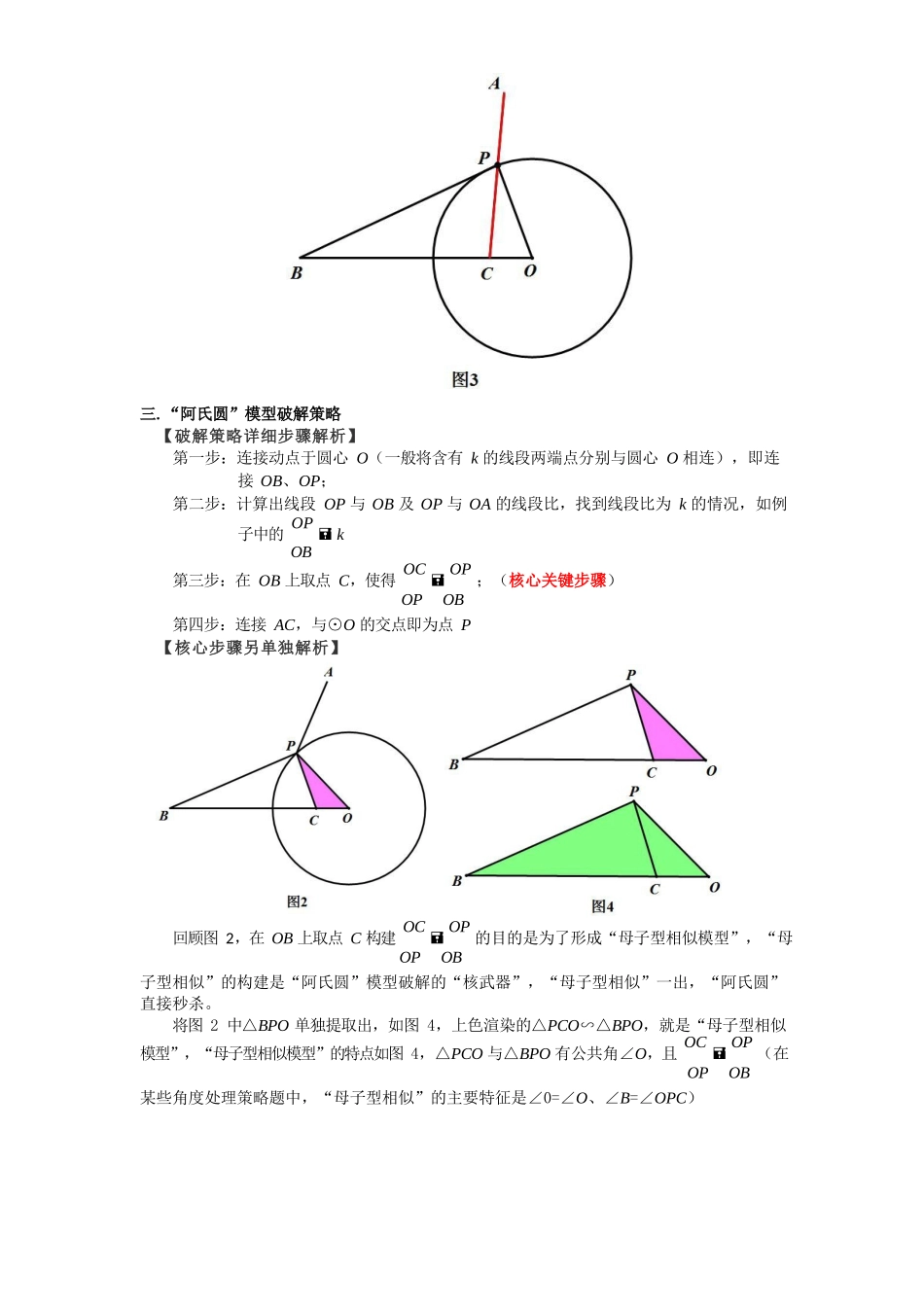
一.模型名称由来经典几何模型之“阿氏圆”————段廉洁【模型背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。当 k值为 1 时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“饮马问题”模型来处理,即可以转化为轴对称问题来处理。而当 k 取任意不为 1 的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。此类问题的处理通常以动点 P 所在图像的不同来分类,一般分为 2 类研究。即点 P 在直线上运动和点 P在圆上运动。其中点 P 在直线上运动的类型称之为“胡不归”问题;点 P 在圆周上运动的类型称之为“阿氏圆” 问题。【模型由来】“阿氏圆”又称“阿波罗尼斯圆”,已知平面上两点 A、B,则所有满足 PA=k· PB(k≠1)的点 P 的轨迹是一个圆,这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”。二.模型建立如图 1 所示,⊙O 的半径为 r,点 A、B 都在⊙O 外,P 为⊙O 上一动点,已知 r=k·OB,连接 PA、PB,则当“PA+k·PB”的值最小时,P 点的位置如何确定?模型解读:最早见“PA+PB”型问题应该是在“将军饮马”问题中,而本题多了一个“k”,故如何确定“k·PB”的大小是关键,如图 2,在线段 OB 上截取 OC 使 OC=k·r,则可说明△BPO 与△PCO 相似,即 k·PB=PC。故本题求“PA+k·PB”的最小值可以转化为 “PA+PC”的最小值,其中与 A 与 C 为定点,P 为动点,故当 A、P、C 三点共线时, “PA+PC”值最小。如图 3三.“阿氏圆”模型破解策略【破解策略详细步骤解析】第一步:连接动点于圆心 O(一般将含有 k 的线段两端点分别与圆心 O 相连),即连接 OB、OP;第二步:计算出线段 OP 与 OB 及 OP 与 OA 的线段比,找到线段比为 k 的情况,如例子中的 OP kOB第三步:在 OB 上取点 C,使得 OC OP ;(核心关键步骤)OPOB第四步:连接 AC,与⊙O 的交点即为点 P【核心步骤另单独解析】回顾图 2,在 OB 上取点 C 构建 OC OP 的目的是为了形成“母子型相似模型”,“母OPOB子型相似”的构建是“阿氏圆”模型破解的“核武器”,“母子型相似”一出,“阿氏圆”直接秒杀。将图 2 中△BPO 单独提取出,如图 4,上色渲染的△PCO∽△BPO,就是“母子型相似模型”,“母子型相似模型”的特点如图 4,△PCO 与△BPO 有公共角∠O,且 OC OP (在OPOB某些角度处理策略题...