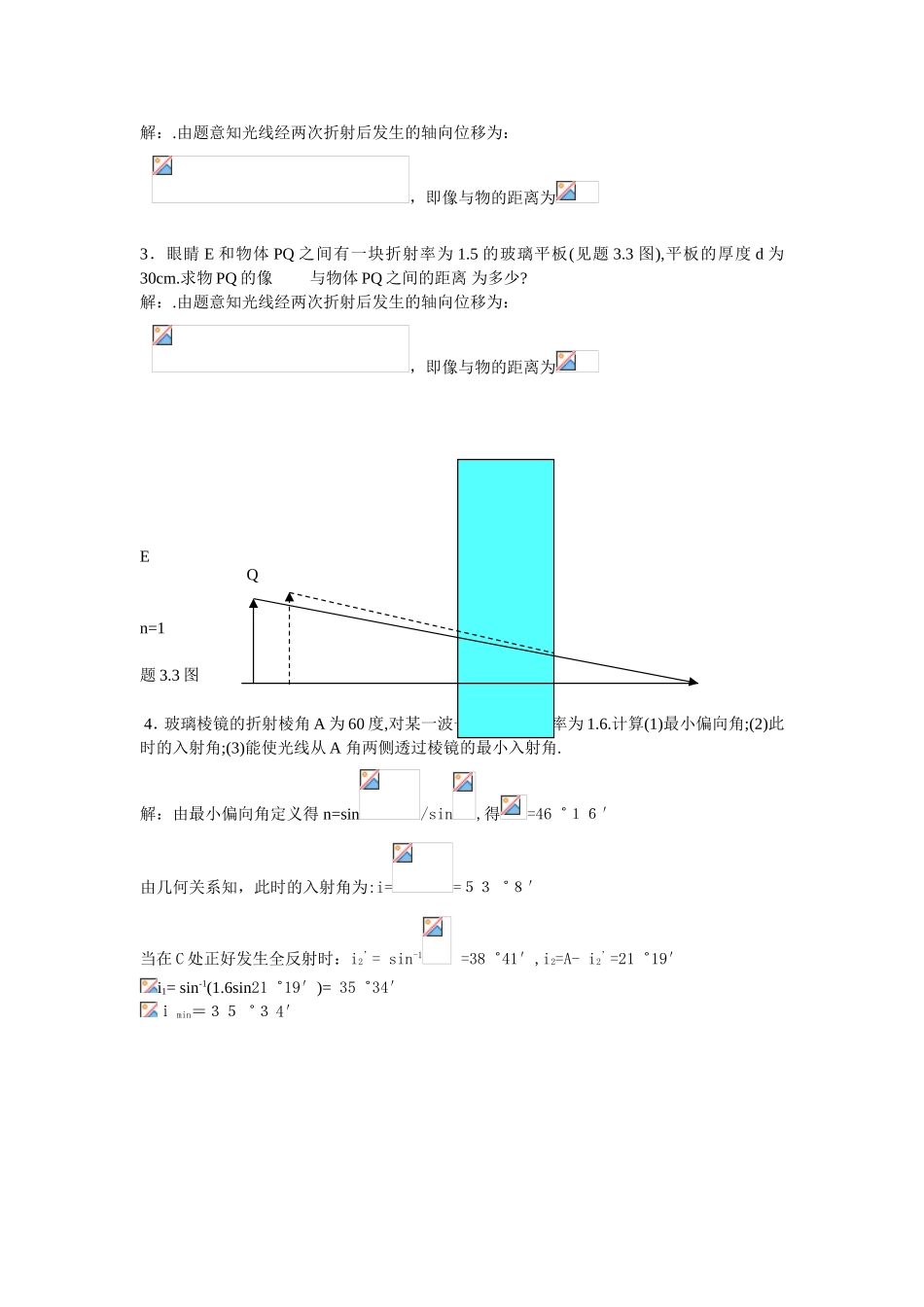
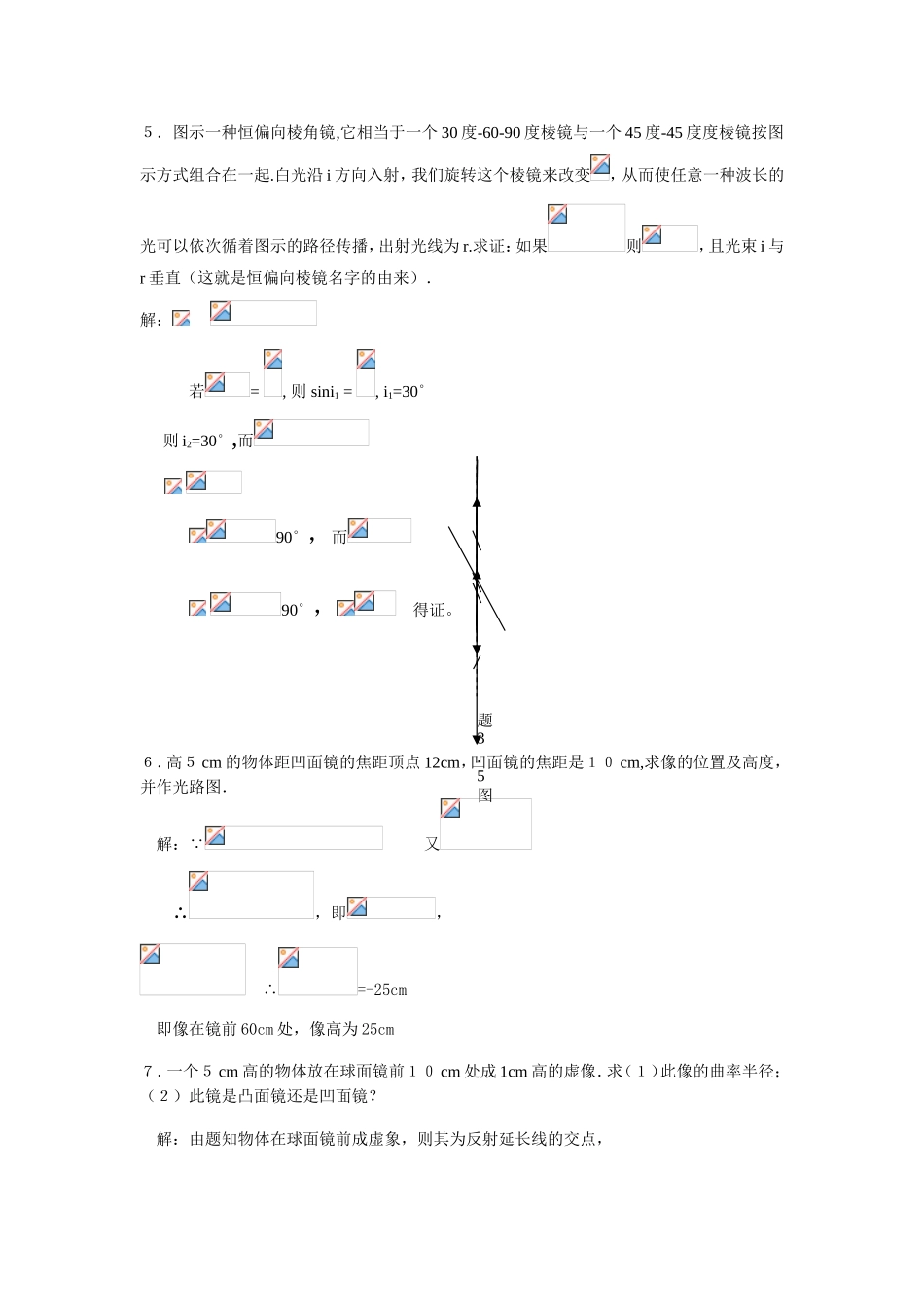
几何光学习题及解答1.证明反射定律符合费马原理。证明:费马原理是光沿着光程为最小值、最大值或恒定值的路径传播。,在介质n与的界面上,入射光A遵守反射定律,经O点到达B点,如果能证明从A点到B点的所有光程中AOB是最小光程,则说明反射定律符合费马原理。设C点为介质分界面上除O点以外的其他任意一点,连接ACB并说明光程ACB>光程AOB由于ACB与AOB在同一种介质里,所以比较两个光程的大小,实际上就是比较两个路程ACB与AOB的大小。从B点到分界面的垂线,垂足为,并延长至B′,使,连接,根据几何关系知,再结合,又可证明∠°,说明三点在一直线上,与AC和组成Δ,其中。又 即符合反射定律的光程是从A点到B点的所有光程中的极小值,说明反射定律符合费马原理。2、根据费马原理可以导出在近轴光线条件下,从物点发出并会聚到像点的所有光线的光程都相等.由此导出薄透镜的物象公式。证明:由QBA~FBA得:OF\AQ=BO\BQ=f\s同理,得OA\BA=\,BO\BA=f\s由费马定理:NQA+NQ=NQ结合以上各式得:(OA+OB)\BA=1得证3.眼睛E和物体PQ之间有一块折射率为1.5的玻璃平板(见题3.3图),平板的厚度d为30cm.求物PQ的像与物体PQ之间的距离为多少?CAOBO‘B‘••O••题3.19图••••ii’nn’解:.由题意知光线经两次折射后发生的轴向位移为:,即像与物的距离为3.眼睛E和物体PQ之间有一块折射率为1.5的玻璃平板(见题3.3图),平板的厚度d为30cm.求物PQ的像与物体PQ之间的距离为多少?解:.由题意知光线经两次折射后发生的轴向位移为:,即像与物的距离为En=1题3.3图4.玻璃棱镜的折射棱角A为60度,对某一波长的光其折射率为1.6.计算(1)最小偏向角;(2)此时的入射角;(3)能使光线从A角两侧透过棱镜的最小入射角.解:由最小偏向角定义得n=sin/sin,得=46゜16′由几何关系知,此时的入射角为:i==53゜8′当在C处正好发生全反射时:i2’=sin-1=38゜41′,i2=A-i2’=21゜19′i1=sin-1(1.6sin21゜19′)=35゜34′imin=35゜34′Q5.图示一种恒偏向棱角镜,它相当于一个30度-60-90度棱镜与一个45度-45度度棱镜按图示方式组合在一起.白光沿i方向入射,我们旋转这个棱镜来改变,从而使任意一种波长的光可以依次循着图示的路径传播,出射光线为r.求证:如果则,且光束i与r垂直(这就是恒偏向棱镜名字的由来).解:若=,则sini1=,i1=30。则i2=30。,而90。,而90。,得证。6.高5cm的物体距凹面镜的焦距顶点12cm,凹面镜的焦距是10cm,求像的位置及高度,并作光路图.解: 又∴,即,∴=-25cm即像在镜前60cm处,像高为25cm7.一个5cm高的物体放在球面镜前10cm处成1cm高的虚像.求(1)此像的曲率半径;(2)此镜是凸面镜还是凹面镜?解:由题知物体在球面镜前成虚象,则其为反射延长线的交点,题3.5图 ∴,又,∴,所以此镜为凸面镜。8.某观察者通过一块薄玻璃板去看凸面镜中他自己的像.他移动着玻璃板,使得在玻璃板中与在凸面镜中所看到的他眼睛的像重合在一起,若凸面镜的焦距为10cm,眼睛距凸面镜顶点的距离灵40cm,问玻璃板观察者眼睛的距离为多少?解:根据题意,由凸面镜成像公式得:∴凸透镜物点与像点的距离,则玻璃距观察者的距离为9.物体位于凹面镜轴线上焦点之外,在焦点与凹面镜之间放一个与轴线垂直的两表面互相平行的玻璃板,其厚度为d1,折射率为n.试证明:放入该玻璃板后使像移动的距离与把凹面镜向物体移动d(n-1)/n的一段距离的效果相同。解:证明:将玻璃板置于凹面镜与焦点之间,玻璃折射成像,由三题结果得d=d(1-1\n),即题中所求。10.欲使由无穷远发出的近轴光线通过透明球体并成像在右半球面的顶点处,问这透明球体的折射率为多少?解:设球面半径为r,物距和相距分别为s和,由物像公式:S=,=2r,n=1,得=211.有一折射率为1.5,半径为4cm的玻璃球,物体在距球表面6cm处,求(1)物所在的像到球心之间的距离;(2)像的横向放大率.解:的玻璃球。对第一个球面,,对第二个球面∴∴∴从物成的像到球心距离12.一个折射率为1.53,直径为20cm的玻璃球内有两个小气泡.看上去一个恰好在球心,另一个从最近的方向看去,好像在表面与球心连线的中点.求两气泡的实际位置解:由球面镜成像公式:,当=...