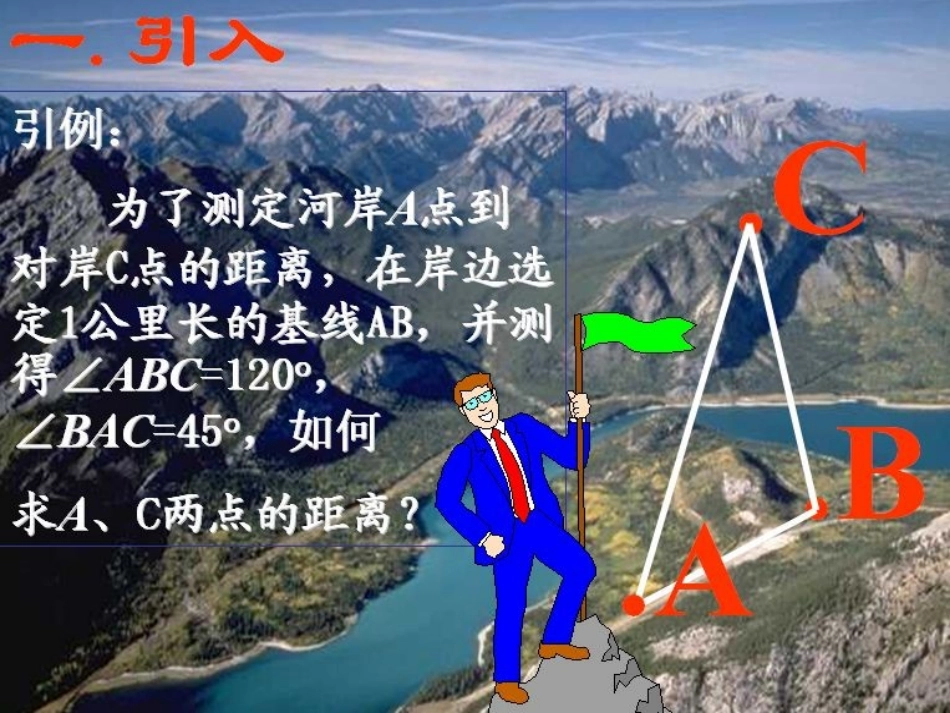
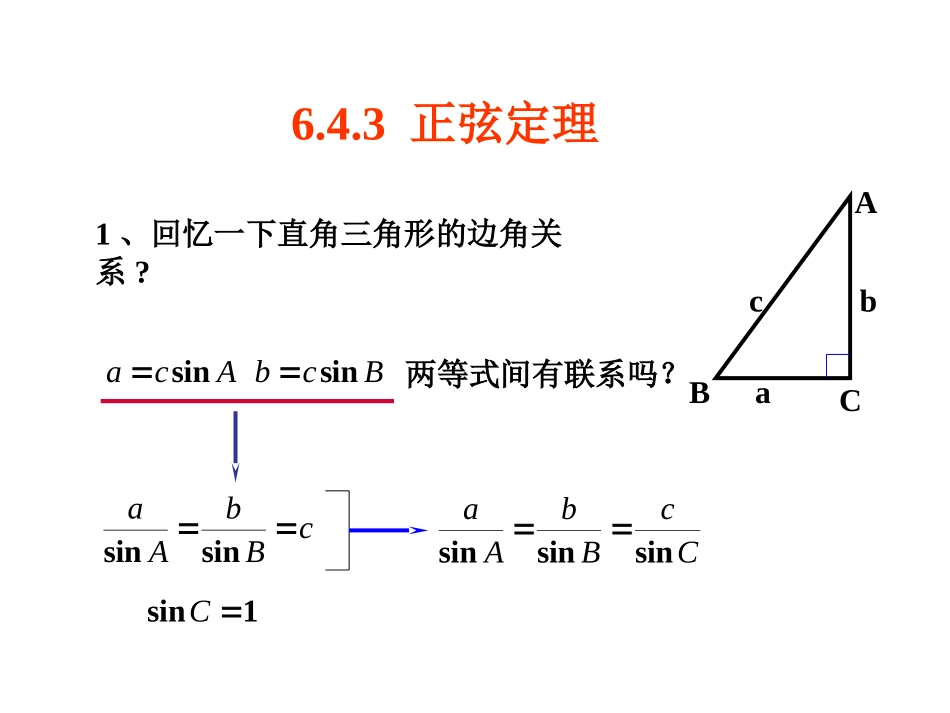
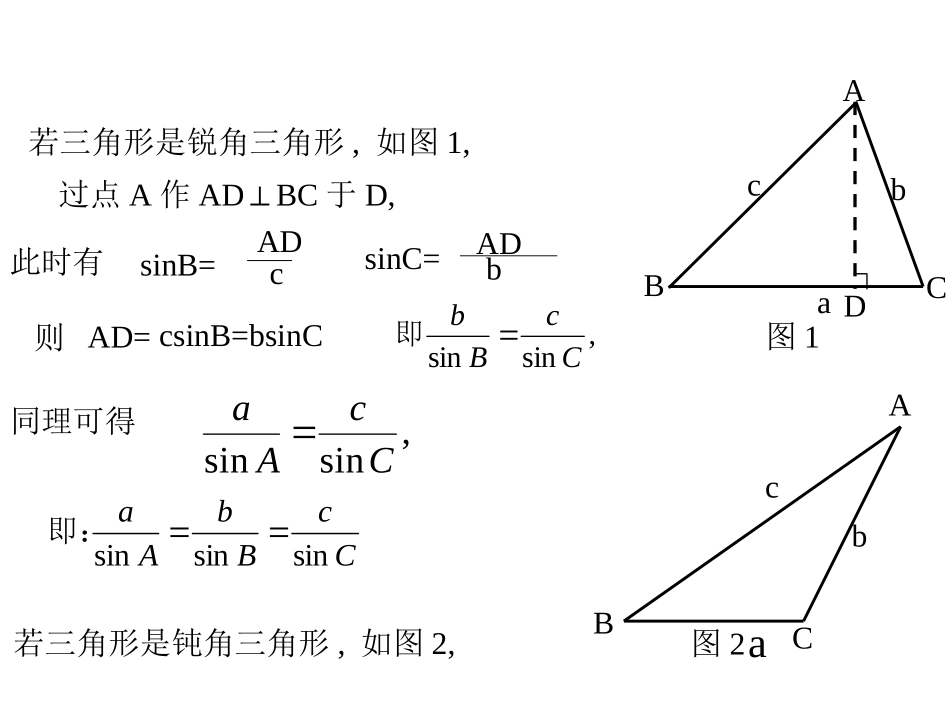
1.1正弦定理1、回忆一下直角三角形的边角关系?ABCcbaAcasinBcbsin两等式间有联系吗?cBbAasinsin1sinCCcBbAasinsinsin6.4.3正弦定理csinB=bsinC,sinsinCcBb即同理可得,sinsinCcAaCcBbAasinsinsin即:D过点A作ADBC⊥于D,此时有若三角形是锐角三角形,如图1,若三角形是钝角三角形,如图2,AcbCB图1asinB=ADcsinC=ADb则AD=CAcbB图2aCcBbAasinsinsin正弦定理在一个三角形中,各边和它所对角的正弦的比相等,即注:每个等式可视为一个方程:知三求一要牢记哟!边和它所对角的正弦比相等一般地,把三角形的三个角A,B,C和他们的边a,b,c叫做三角形的元素,已知三角形的几个元素,求其他元素的过程叫做解三角形.•利用正弦定理可以解决一些怎样的解三角形问题呢?例2、在△ABC中,已知32a,b=6,A=30,已知两边和其中一边的对角,可以求出三角形的其他的边和角(1)求B(2)求C和c例在中,已知,求b.ABC30,45,10CAcCBAabc已知两角和任意边,求其他两边和一角例3、为了测定河岸A点到对岸C点的距离,在岸边选定1公里长的基线AB,并测得∠ABC=120°BCA=45°,∠求A,C两点的距离解:由正弦定理得AB=ACsinCsinB则AC=ABsinBsinC求出AC=62ABC120°45°11、在中,一定成立的等式是()ABCBbAaAsinsin.BbAaBcoscos.AbBaCsinsin.AbBaDcoscos.C随堂练习2、在△ABC中已知a=18,B=60°,C=75°,求b=963、已知c=,A=45°,B=75°,则a=____,32D4、△ABC中,B=30°,c=150,b=50,则△ABC的形状是()3A等边三角形B等腰三角形C直角三角形D等腰或直角三角形5、△ABC中,已知a=2,b=2,A=45°,则B=60°或120°236、已知c=2,A=120°,a=,则B=____3230°7、△ABC中,a=50,b=25,A=45°,求B6五、小结1、这节课我们主要学习了正弦定理,以及两类应用正弦定理解决的解三角形问题.2.通过本节课学习,在研究数学问题时要掌握从特殊到一般、数形结合以及分类讨论的数学思想.