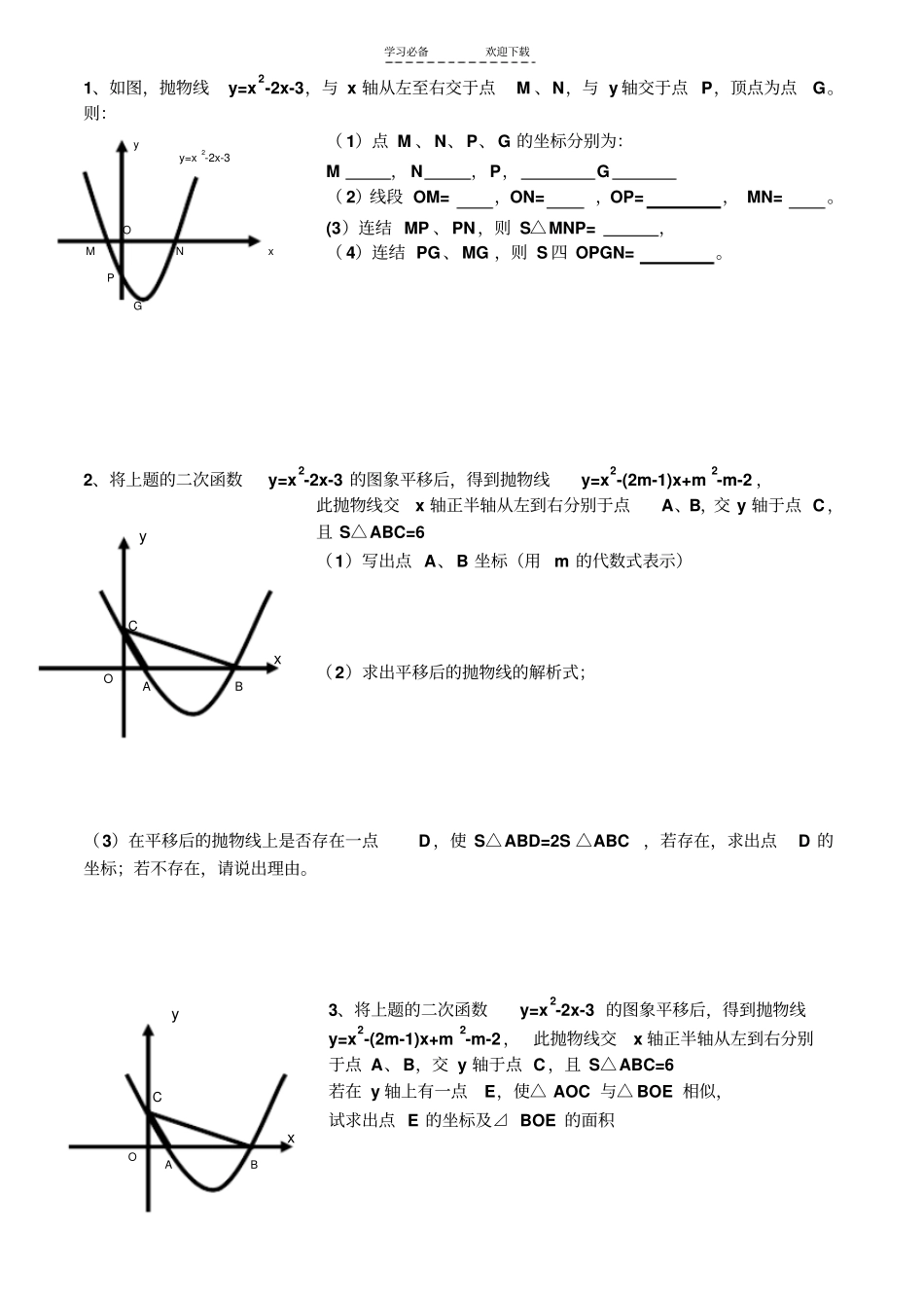
学习必备欢迎下载坐标准系中有关面积的计算题1、直线 y=x+1 与抛物线y=x2 的交点分别为A、B,求△ AOB 的面积2、直线 y= -2 x+1 与抛物线y=x2-2 的交点分别为A、B,抛物线 y=x2-2 与 y 轴的交点为C,求△ ACB 的面积3、抛物线y=(x+1)2-4 与 x 轴交于 A,B,点 A 在点 B 的左侧,抛物线与y 轴交于点 C,抛物线的顶点为D,求四边形ABCD 的面积,△ ACD 的面积。4、如图,在直角坐标系xoy 中,O 是坐标原点,抛物线y=x2-x-6 与 x 轴交于 A、B 两点(点A 在点 B 的左侧),与 y 轴交于点 C,如果点 M 在 y 轴右侧的抛物线上,且 S△AMO =32 S△COB,求点 M 的坐标OACB学习必备欢迎下载1、如图,抛物线y=x2-2x-3,与 x 轴从左至右交于点M 、N,与 y 轴交于点 P,顶点为点G。则:( 1)点 M 、N、P、G 的坐标分别为:M , N ,P,G ( 2)线段 OM=,ON=,OP= , MN=。(3)连结 MP 、PN,则 S△MNP= ,( 4)连结 PG 、MG ,则 S 四 OPGN= 。2、将上题的二次函数y=x2-2x-3 的图象平移后,得到抛物线y=x2-(2m-1)x+m2-m-2 ,此抛物线交x 轴正半轴从左到右分别于点A、B,交 y 轴于点 C,且 S△ABC=6 (1)写出点 A、B 坐标(用 m 的代数式表示)(2)求出平移后的抛物线的解析式;(3)在平移后的抛物线上是否存在一点D,使 S△ABD=2S △ABC ,若存在,求出点D 的坐标;若不存在,请说出理由。3、将上题的二次函数y=x2-2x-3 的图象平移后,得到抛物线y=x2-(2m-1)x+m2-m-2 , 此抛物线交x 轴正半轴从左到右分别于点 A、B,交 y 轴于点 C,且 S△ABC=6 若在 y 轴上有一点E,使△ AOC 与△ BOE 相似,试求出点 E 的坐标及⊿ BOE 的面积x y M N P G O y=x2-2x-3 O C A B x y O C A B x y