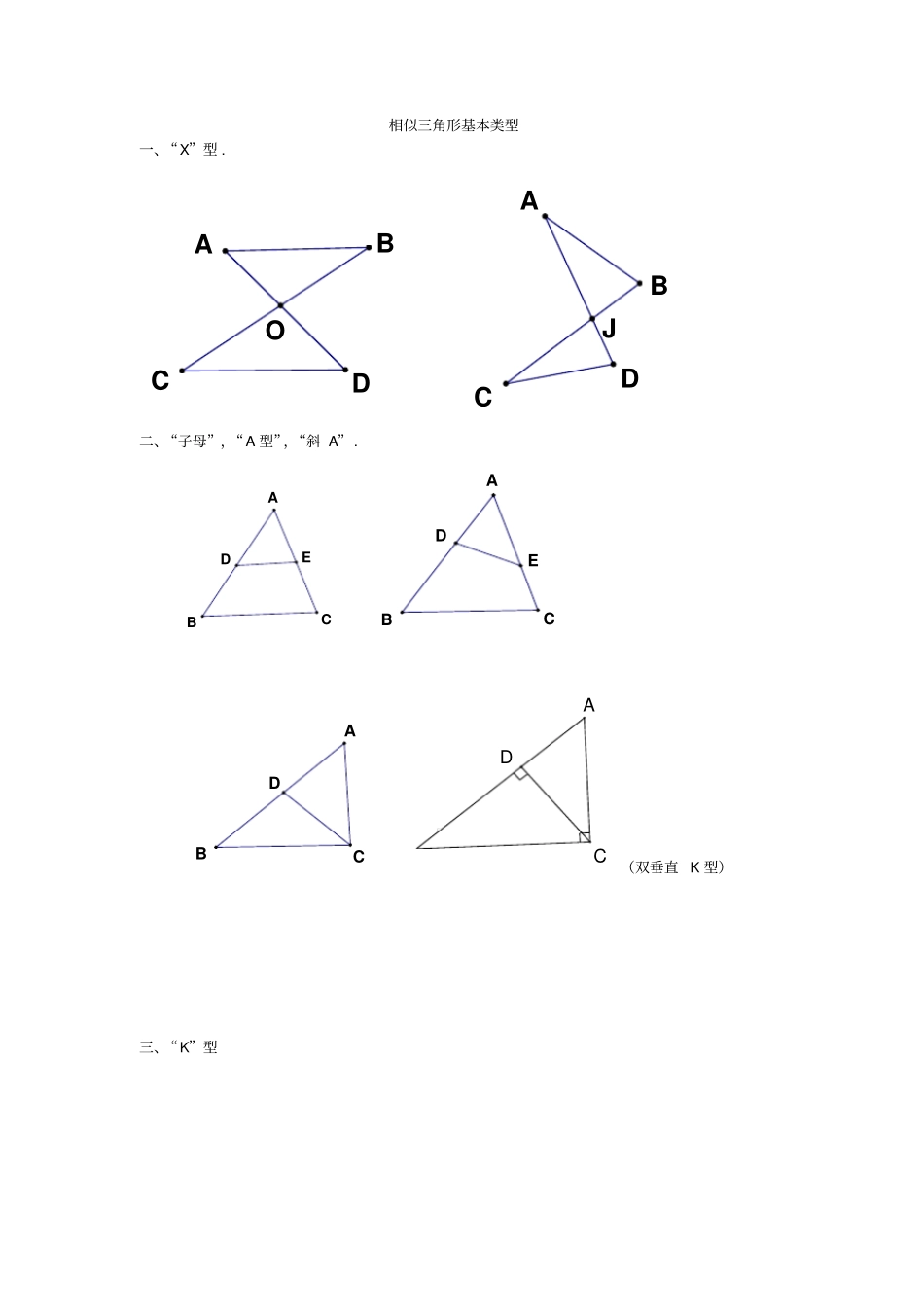
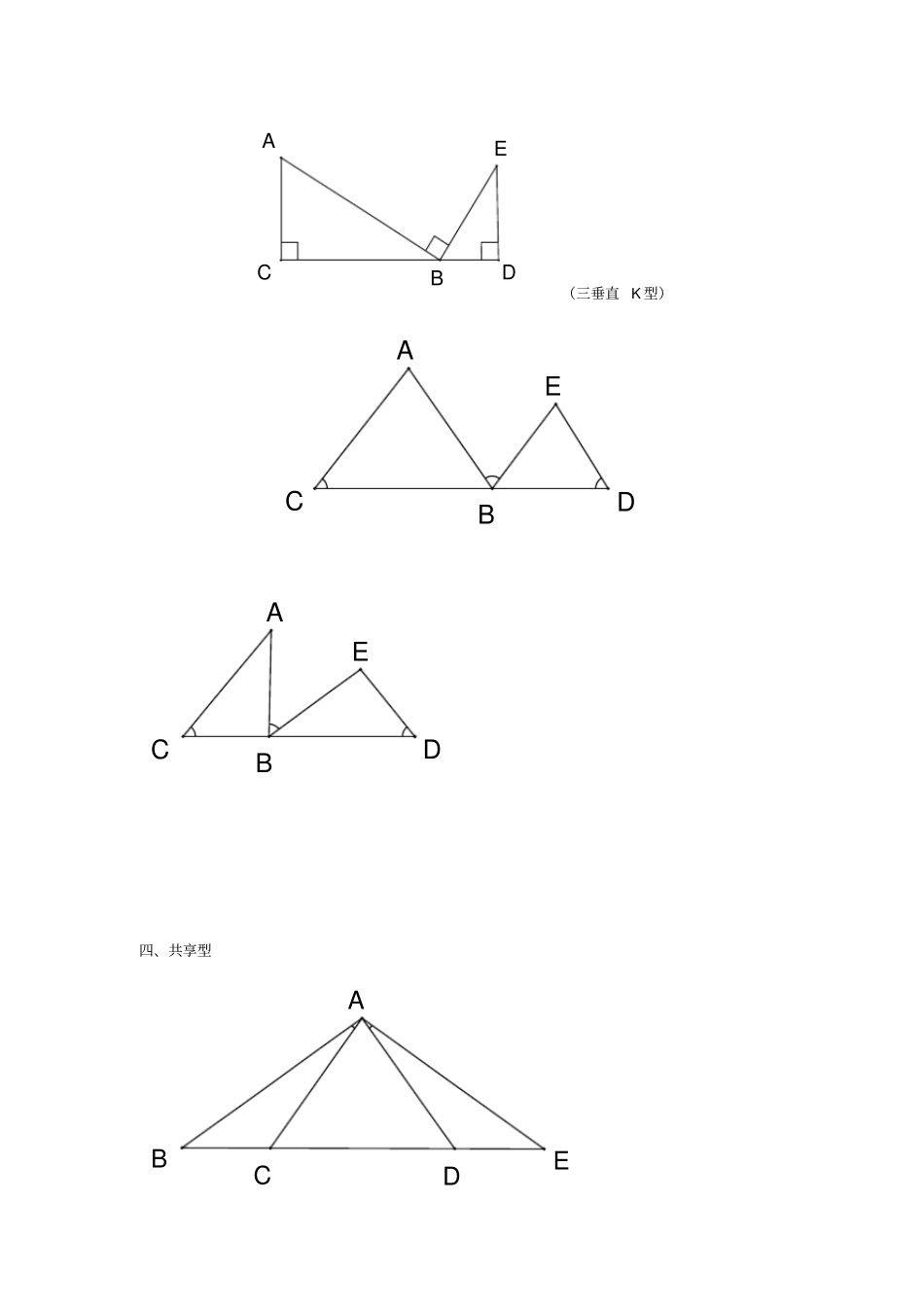
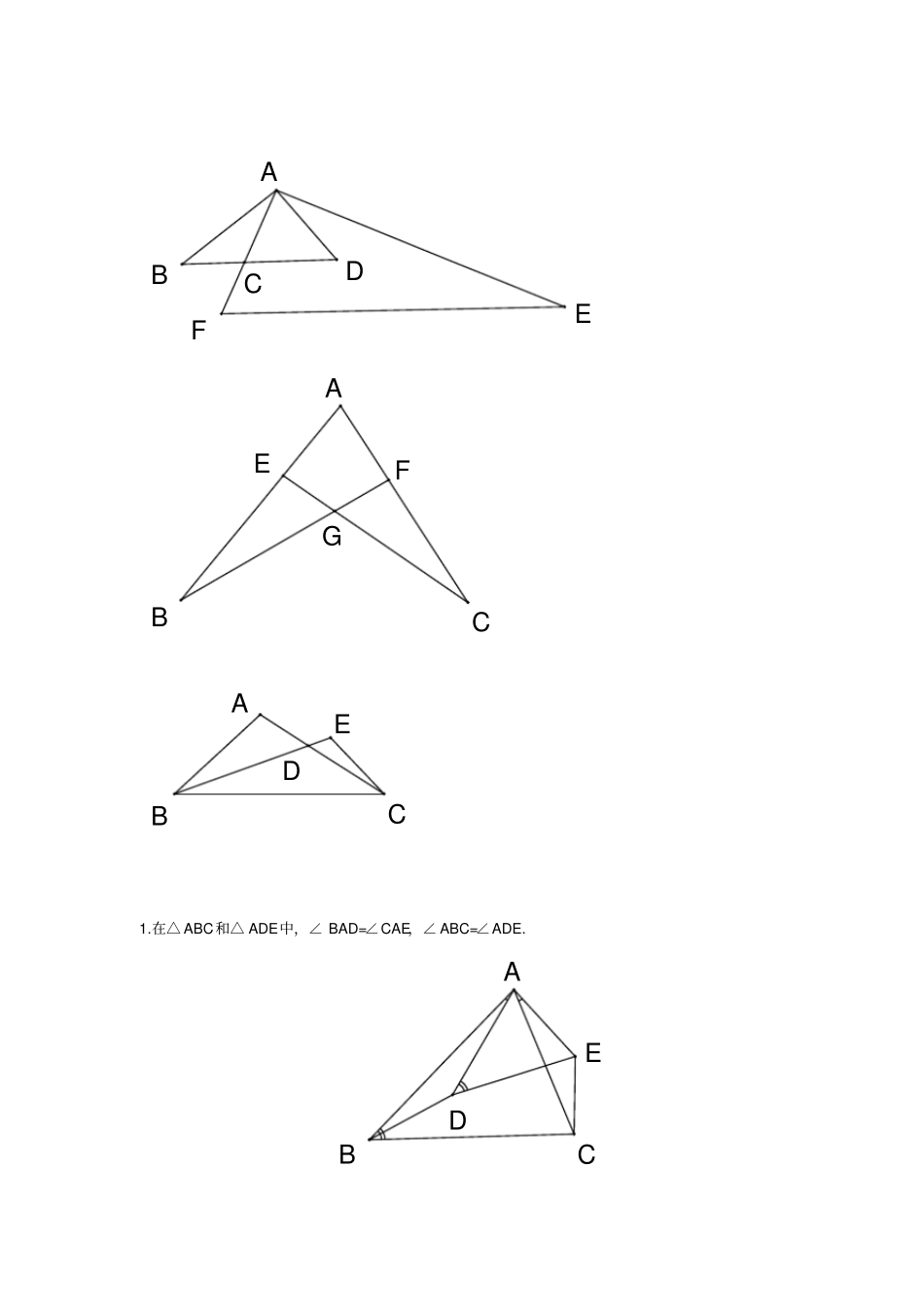
相似三角形基本类型一、“X”型 . JOADBCABCD二、“子母”,“A 型”,“斜 A”. ABCDECBADEABCDCAD(双垂直 K 型)三、“K”型ACDEB(三垂直 K 型)ACDEBCAEBD四、共享型ABECDCABDFEGABCEFDBCAE1.在△ ABC和△ ADE中,∠ BAD=∠CAE,∠ ABC=∠ADE. ABCDE1.如图,已知∠ 1=∠2,∠ 3=∠ 4,求证∠ ABE=∠ACD. 4321FABDCE2. EFGTABOP3.如图,已知C 是线段 AB 上的任意一点(端点除外),分别以AC、BC为斜边并且在AB 的同一侧作等腰直角△ACD和△ BCE,连结 AE交 CD于点 M ,连结 BD 交 CE于点 N,给出以 下三个结论:①MN ∥AB;②1MN=1AC+1BC;③ M N≤14AB,其中正确结论的个数是()A.0 B.1 C.2 D.3 FECBAB'C'4.如图, Rt△AB C 是由 Rt△ABC绕点 A 顺时针旋转得到的,连结CC 交斜边于点E,CC 的延长线交BB 于点 F.(1)证明:△ ACE∽△ FBE;(2)设∠ ABC=,∠ CAC =,试探索、满足什么关系时,△ACE与△ FBE是全等三角形,并说明理由.5. Q2AEFDBC6.在等边△ ABC中,D 为 BC边上一点, E为 AC边上一点,且∠ADE=60° , BD=3,CE=2,则△ABC的边长为 _________. ABCDE7. 090AE° , 12EDBC . (1)当 AB=AC时,①∠ EBF=_________. ② BE与 FD数量关系 . (2)当 AB=kAC,求 BEFD的值 . FBECADFBACED8. 如图,梯形ABCD中, AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从 B、D两点同时..出发,点 P以每秒 2cm的速度沿 BC向终点 C移动,点 Q以每秒 1cm的速度沿 DA 向终点 A 移动,线段PQ与 BD相交于点 E,过 E作 EF∥BC交 CD于点 F,射线 QF交 BC的延长线于点 H,设动点 P、Q移动的时间为t (单位:秒, 0